Horn Clause Transformation for Program Verification

By Emanuele De Angelis, Fabio Fioravanti DEC, University ‘G. d’Annunzio’, Chieti-Pescara, Italy
Alberto Pettorossi DICII, University  ‘Tor Vergata’ and IASI-CNR, Rome, Italy
Maurizio Proietti IASI-CNR, Rome, Italy

1 Introduction

Horn clauses and constraints have been advocated by many researchers as suitable
logical formalisms for the specification and the automated verification of properties of
imperative programs [1, 2, 5, 15, 16, 17, 19, 20]. Indeed, the verification conditions
(or assertions) that express the correctness of a given program, can often be written
as implications of the form

A₀ ← c,A₁,…,A_n

where A₀ is either an atomic formula or false, c is a constraint in a suitable first order
theory, and A₁,…,A_n are atomic formulas. For instance, consider the following C-like

program prog:

x = 0;  y = 0;

while (x < n) { x = x + 1; y = y + 2 }

and assume that we want to prove the following Hoare triple: {n ≥1}prog{y > x}.
This triple is valid if the set consisting of the following verification conditions is
satisfiable:

C1.  p(X,Y,N) ←X = 0,Y = 0,N ≥1

C2.  p(X + 1,Y + 2,N) ←X < N,p(X,Y,N)

C3.  false ←X ≥N,Y ≤X,p(X,Y,N)

Clauses C1–C3 state that p(X,Y,N) is a loop invariant, which holds upon initialization (clause C1), is preserved during the loop (clause C2), and implies the postcondition Y > X upon exit, when X ≥N holds (clause C3).

Recently, in the literature on automated program verification the term Constrained Horn Clauses (CHCs) has been used to denote the class of logical formulas such as clauses C1–C3 above, with constraints in arbitrary theories (not integer arithmetics only). Thus, CHCs are syntactically the same as Constraint Logic= Programs [14]. However, the term Constraint Logic Program evokes an operational interpretation based on a refutation procedure (that is, a procedure for proving the unsatisfiability of a set of formulas), while the term Constrained Horn Clauses has no operational implication. Moreover, many techniques for Constrained Horn Clauses search for a model, expressible in the constraint theory, that proves the satisfiability of the clauses.

A large variety of CHC solvers have been developed to verify the satisfiability of
sets of Constrained Horn Clauses modulo various theories: (linear or non-linear)
integer arithmetics, real (or rational) arithmetics, booleans, integer arrays, lists,
heaps, and other data structures [3, 10, 12, 13].

Note that in the example above, the evaluation of the goal consisting of clause R3
will not terminate using standard Constraint Logic Programming systems. Tabling
will not help either, as infinitely many answers should be memoized. In contrast, CHC
solvers will prove satisfiability by making use of constraint-based abstraction
techniques.

2 A Transformation-Based Approach to Program Verification

In the last few years we have developed an approach for the verification of
imperative programs that combines well-established techniques introduced in
the field of analysis and transformation of Constraint Logic Programming
and techniques for CHC solving [5, 6, 7, 8, 9]. Our approach, depicted in
Figure 1, is parametric with respect to both: (i) the programming language, and
(ii) the class of properties to be verified, as long as they can be encoded as
CHCs.

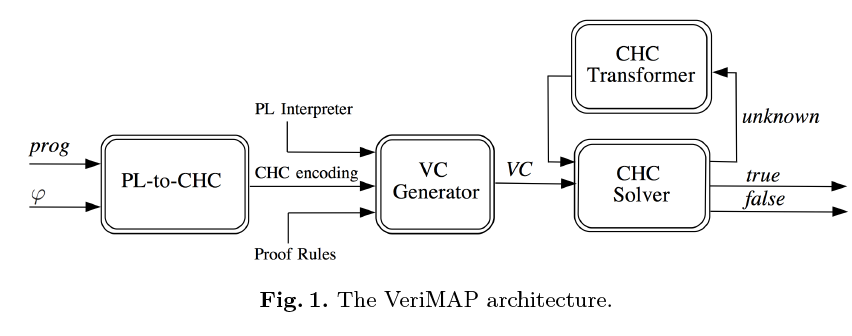
Suppose we are given a program prog in a programming language PL and a
property φ in a class Φ of properties. The system for automatically verifying whether
or not prog satisfies φ is made out of the following four components.

1.

A translator from PL and Φ (see the ‘PL-to-CHC’ box), that constructs a
CHC encoding of prog and φ.

2.

A Verification Condition Generator (see the ‘VC Generator’ box), that takes
as input (i) the CHC encoding of prog and φ, (ii) a set of CHCs that encode
an interpreter for PL, and (iii) a set of CHCs that encode the proof rules
for proving formulas in Φ. The output of the VC Generator is a set VC
of verification conditions for prog and φ, that is, a set of CHCs which is
satisfiable if and only if φ holds for prog.

3.

A solver for Constrained Horn Clauses (see the ‘CHC Solver’ box), that
checks the satisfiability of VC. The output can be true (φ holds for prog),
false (φ does not hold for prog), or unknown (the CHC solver was not able to
prove satisfiability or unsatisfiability with the given computing resources).
Since the satisfiability of CHCs is, in general, an undecidable property, no
solver can be both complete and terminating, and hence the answer unknown
cannot be avoided.

4.

A transformer for Constrained Horn Clauses (see the ‘CHC Transformer’
box), that works as follows. If the solver returns unknown, then the CHC
transformer derives, from the given set of CHCs, a new, equisatisfiable set
of CHCs by applying some transformation rules, such as unfolding and
folding [11], under the guidance of suitable transformation strategies. The
objective of this transformation is to derive a new set of CHCs for which,
hopefully, the solver is able to return either true or false. The loop consisting
of an application of the CHC Solver, possibly followed by an application of
the CHC Transformer, may be iterated until we get either a definite answer
(that is, true or false) or we exhaust the computing resources.

3 Generating Verification Conditions by Specializing Interpreters

The translation of the programs written in the programming language PL and the
properties in the class Φ to CHCs consists in a change of representation that can be
realized by using standard parsing and translation tools [18].

The VC Generator has a much more crucial role in our approach, as it ensures the
parametricity with respect to the programming language PL and the class Φ of
properties. The parametricity with respect to the programming language is achieved
by following a method first proposed by Peralta et al. [19], which makes use of a
specialization transformation technique. Indeed, the VC Generator takes as input an

interpreter of PL written as a set of CHCs (which can be viewed as a logic program
executing the imperative program), and then it specializes the interpreter with
respect to the specific program prog to be verified (which can be viewed as the input
to the CHC interpreter). This approach has been shown to be effective and scalable
for developing analysis and verification techniques for several languages, such as C,
Java, and Java bytecode, and for several styles of presenting the operational
semantics of a programming language, such as the small-step or big-step
semantics [1, 5, 8, 17].

In the case of an imperative language with the small-step semantics, the CHC
interpreter encodes a binary transition relation tr between configurations,
representing states of the program execution. To get an idea of how the interpreter is
written, now we give the semantic rule for the labelled assignment ℓ :  x := e
(assuming that the program in which it occurs is a sequence of labelled commands).

tr(cf (cmd(L,asgn(X,expr(E))),Env),cf (cmd(L1,C),Env1)) ←

  eval(E,Env,V ),update(Env,X,V,Env1),nextlab(L,L1),at(L1,C)

Configurations are represented by terms of the form cf (cmd(L,C),Env), where: (i)
cmd(L,C) encodes a command C with label L, and (ii) Env encodes the
environment as a list of ⟨variable identifier,value⟩ pairs. The term asgn(X,expr(E))
encodes the assignment of the value of the expression E to the variable identifier X.
The predicate eval(E,Env,V ) holds iff V is the value of the expression E in the
environment Env. The predicate update(Env,X,V,Env1) holds iff Env1 is the
environment obtained by replacing the value of the variable identifier X in
the environment Env by the new value V. nextlab(L,L1) holds iff L1 is the
label of the command textually following the command with label L in the
given program. at(L1,C) holds iff C is the command at label L1 in the given
program.

The parametricity with respect to the class of properties is achieved by following a
similar approach: the VC Generator takes as input the proof rules, written as
CHCs, for the properties in Φ, and then specializes them with respect to φ.
For instance, the validity of a Hoare triple can be encoded by the following
clauses:

R1.  reachFromInit(C) ← initConf (C)

R2.  reachFromInit(C1) ← tr(C,C1),reachFromInit(C)

R3.  false ← errorConf (C),reachFromInit(C)

where: (i) initConf (C) states that C is an initial configuration for which the
precondition holds, (ii) reachFromInit(C) states that configuration C is reachable
from an initial configuration, and (iii) errorConf (C) states that C is a final
configuration for which the postcondition does not hold.

By specializing the clauses R1–R3, together with the clauses for the interpreter
which define the predicate tr, with respect to the Hoare triple considered in
the introductory example, we automatically derive clauses C1–C3 shown in
the Introduction. Note that the specialization removes all the references
to the interpreter, and for this reason it is also called the removal of the
interpreter.

4 Improving CHC Solving via CHC Transformation

The set VC of verification conditions derived via specialization by the VC Generator
can be given as input to any CHC Solver with a suitable underlying constraint theory
(the theory of linear integer arithmetics, in our introductory example). However, the
CHC solver may neither be able to prove the satisfiability of VC, and find a model
expressible in the constraint theory, nor be able to prove the unsatisfiability of
VC.

If this is the case, we can apply some transformation techniques that preserve
satisfiability, that is, derive a set of clauses which is satisfiable if and only if VC is
satisfiable, and by doing so, we hopefully simplify the satisfiability problem to be
given as input to the CHC solver. Below we briefly describe some of these
techniques.

Constraint Propagation. This transformation is a specialization technique
that propagates the constraints occurring in the goals belonging to VC. This
transformation works by unfolding the goals of VC, and by introducing specialized
versions of the predicates derived by unfolding. One effect of Constraint Propagation
is that the clauses defining the specialized predicates may have stronger constraints
with respect to those occurring in the original clauses.

Clause Removal. We can remove clauses which are trivially satisfiable because they
have inconsistent constraints in their body. Another case where we can remove a set
of clauses and preserve satisfiability, is when these clauses define a useless predicate.
The set of useless predicates in a given set Q of CHCs is the largest set U
of predicates occurring in Q such that p is in U iff every clause with
head predicate p is of the form p(X) ← c,G₁,q(Y),G₂,  for some q in U.

Clause Reversal. It is often useful to propagate the constraints that occur in
constrained facts, that is, in clauses of the form A ← c, where c is a constraint. This
particular propagation can be performed by applying Constraint Propagation after a
transformation, called Reversal, that interchanges the roles of the goals and
constrained facts. For instance, by applying the Reversal transformation to clauses
R1–R3 of Section 3, we get:

RR1.  reachFromError(C) ← errorConf (C)

RR2.  reachFromError(C) ← tr(C,C1),reachFromError(C1)

RR3.  false ← initConf (C),reachFromError(C)

Note that also the arguments of reachFromError in the head and body of clause RR2,
respectively, are interchanged with respect to those of reachFromInit in clause R2.
From the operational point of view, Clause Reversal reverses the flow of computation:
the top-down evaluation (from the goal) of the transformed set of clauses
RR1–RR3 corresponds to the bottom-up evaluation of the original clauses
R1–R3.

Constraint Propagation, Clause Removal, and Clause Reversal can drastically
simplify the task of verifying satisfiability. Indeed, by repeated applications of those
transformations (see, in particular, the Iterated Specialization strategy [5]) we may

derive a new set of verification conditions, call it VC^′, such that VC′ either contains
the clause false ←, and hence VC′ is unsatisfiable, or contains no clauses with head
false, and hence VC′ is satisfiable.

Predicate Pairing. This strategy pairs together two predicates, say q and r, into one
new predicate t equivalent to their conjunction. The clauses defining the new
predicate t are derived from those of q and r by applying the unfold/fold
transformation rules. Predicate Pairing may ease the discovery of relations among the
arguments of the two predicates q and r, and hence it may ease the satisfiability
verification. Obviously, pairing may be iterated and more than two predicates may in
general be tupled together.

Predicate Pairing can be applied for deriving linear clauses (clauses with at most
one atom in their body) from non-linear ones. Non-linear clauses appear when we
specify a program property whose preconditions or postconditions are defined by
non-linear recursive predicates, like in the case of the well-known problem of
computing Fibonacci numbers.

Another case where non-linear clauses appear is when we want to prove relational
program properties. Let us consider two programs P1 and P2 with disjoint variables,
and suppose that we want to prove a property of the following form: If a precondition
relates the initial values of the variables of P1 and P2 and the executions of P1 and
P2 both terminate, then a postcondition relates the final values of the variables of P1
and P2. An example of a relational property is program equivalence, which can be
expressed by writing preconditions and postconditions that state that the final values
of the variables of P1 and P2 are pairwise equal if their initial values are
pairwise equal. Other relational properties relate two executions of the same
program, such as monotonicity, injectivity, and functional dependencies between
variables. A relational property can be encoded by a non-linear clause of the
form

false ← pre(X,Y ), p1(X,X′), p2(Y,Y ′), neg–post(X′,Y ′)

where (i) X and Y are the initial values of the variables of program P1 and P2,
respectively; (ii) pre(X,Y ) is the precondition; (iii) neg–post(X′,Y ′) is the negation
of the postcondition, which we assume to be expressible by a constraint;
and (iv) the predicates p1(X,X′) and p2(Y,Y ′) are predicates defining the
input/output relations of programs P1 and P2, respectively, obtained by using the
formalization of the operational semantics of the programming language presented in
Section 3.

Predicate Pairing is able, in some cases, to transform satisfiability problems that
are not solvable by CHC solvers into problems that are solvable. Indeed, we have
shown that many satisfiability problems generated by non-linear postconditions (like,
for instance, those of the Fibonacci numbers) and by relational properties (such as
program equivalence), can be solved by first applying Predicate Pairing, and then
giving the transformed set of clauses as input to a CHC solver over linear integer
arithmetics [6, 9].

5 The VeriMAP System

The VeriMAP tool [4] implements the transformation-based verification framework
presented in the previous sections. It consists of several modules that realize the
boxes presented in Figure 1. Our tool is mainly implemented in Prolog, with
some source code in other languages for interfacing VeriMAP with external
tools.

1.

PL-to-CHC Translator. VeriMAP provides a translator, based on the C
Intermediate Language (CIL) infrastructure [18], that converts the given C
program and property into a CHC encoding suitable for the VC Generator.

2.

VC Generator. VeriMAP provides several back-ends implementing the
specialization strategies to generate the VCs from different formalizations
of the operational semantics of the C language. Some optimizing techniques
enable users to reduce the number of clauses and predicate arguments.

3.

CHC transformer. VeriMAP provides several modules implementing:
(i) transformation strategies, such as Constraint Propagation, Clause
Reversal, Predicate Pairing, (ii) generalization strategies, which are used for
the automatic discovery of predicates corresponding to program invariants
and for guaranteeing the termination of the transformation strategies, (iii)
constraint solvers, which check satisfiability and entailment in the constraint
theory at hand (for example, the integers or the rationals), by using both
native (clpqr and CHR) or external (SMT) solvers, and (iv) constraint
replacement engines, which guide the application of the axioms and the
properties of the data theory under consideration (for example, the theory
of arrays), and their interaction with the constraint theory (for example, the
integers).

4.

CHC solver. VeriMAP provides some interface modules for using external
CHC solvers, that is, modules that translate CHCs into the SMT-LIB format
for Eldarica [13], MathSAT [3], and Z3 [10].

The VeriMAP system is available for downloading at http://map.uniroma2.it/VeriMAP/
or via web-interface at http://map.uniroma2.it/verimapweb. Benchmarks of
hundreds of examples of verification problems are also available at the above
URLs.

6 Conclusions

Recent work in the field of software verification has established a strong connection
between the problem of verifying the correctness of a program and the problem of

checking the satisfiability of Constrained Horn Clauses. By exploiting that connection,
the many techniques developed over the past three decades in the fields of analysis
and transformation of Constraint Logic Programming can be used for automating the
task of software verification.

References