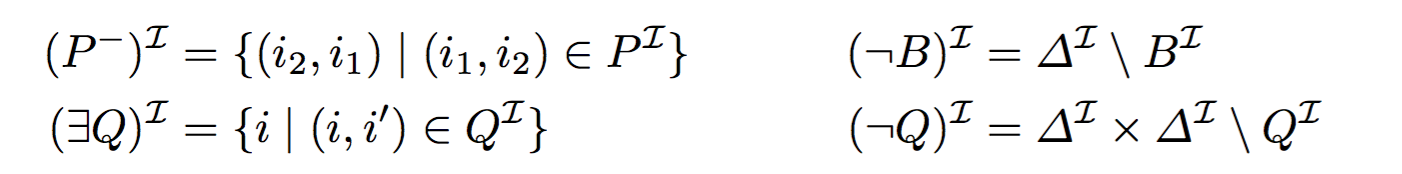NoHR: A Protégé Plugin for Polynomial Querying of Ontologies and Non-Monotonic Rules

By

Matthias Knorr and João Leite
NOVA LINCS, Departamento de Informática,
Faculdade de Ciências e Tecnologia, Universidade Nova de Lisboa

 

PDF VERSION

 

<Note by Editors. Due to the symbols used, the following html conversion of this contribution might be hard to read. In case, read directly the PDF VERSION linked above>

 

1 Introduction

Ontology languages in the form of Description Logics (DLs) [4] and non-monotonic rule languages as known from Logic Programming (LP) [6] are both well-known formalisms in knowledge representation and reasoning (KRR) each with its own distinct benefits and features. This is also witnessed by the emergence of the Web Ontology Language (OWL) [13] and the Rule Interchange Format (RIF) [18] in the ongoing standardization of the Semantic Web driven by the W3C.
On the one hand, ontology languages have become widely used to represent and reason over taxonomic knowledge. Since DLs are (usually) decidable fragments of first-order logic, they are monotonic by nature, which means that drawn conclusions persist when adopting new additional information. Furthermore, they allow reasoning on abstract information, such as relations between classes of objects, even without knowing any concrete instances. The balance between expressiveness and complexity of reasoning with ontology languages, inherited from DLs, is witnessed by the fact that the very expressive general language OWL 2, with its high worst-case complexity, includes three tractable (polynomial) profiles [22] each with a different application purpose in mind.
On the other hand, non-monotonic rules explicitly represent inference, from premises to conclusions, focusing on reasoning over instances. They commonly employ the Closed World Assumption (CWA), i.e., the absence of a piece of information suffices to derive it being false, until new information to the contrary is provided, hence being non-monotonic. This permits to declaratively model defaults and exceptions, in the sense that the absence of an exceptional feature can be used to derive that the (more) common case applies, and also integrity constraints, which can be used to ensure that the data under consideration is conform to the desired specifications.
Combining both formalisms has been frequently requested by applications [24, 25, 1, 26]. For example, in clinical health care, large ontologies such as SNOMED CT, that are captured by the OWL 2 profile OWL 2 EL and its underlying description logic (DL) EL++ [5], are used for electronic health record systems, clinical decision support systems, or remote intensive care monitoring, to name only a few. Yet, expressing conditions such as dextrocardia, i.e., that the heart is exceptionally on the right side of the body, is not possible and requires non-monotonic rules. Another example can be found in [24], where modeling pharmacy data of patients with the closed-world assumption would have been preferred in the study to match patient records with clinical trials criteria, because usually it can be assumed that a patient is not under a specific medication unless explicitly known. In [1] it is shown that in Legal Reasoning, besides the well known need for default reasoning afforded by non-monotonic rules, it is also necessary to reason in the absence of concrete known individuals (instances), hence requiring features found in ontology languages such as DL.
Finding such a combination is a non-trivial problem due to the mismatch between semantic assumptions of the two formalisms, and the considerable differences as to how decidability is ensured in each of them, where a naive combination can easily become undecidable. In recent years, there has been a considerable amount of effort devoted to combining DLs with non-monotonic rules – see, e.g., related work in [10, 23] – but this has not been accompanied by similar variety of reasoners and applications.
In this paper, we describe NoHR (Nova Hybrid Reasoner), a plug-in for the ontology editor Protégé 5.0, that allows the user to query combinations of EL+ ⊥ or DL-LiteR ontologies and non-monotonic rules in a top-down manner.
NoHR is theoretically founded on the formalism of Hybrid MKNF under the well-founded semantics [19] which comes with two main arguments in its favor. First, the overall approach, which was introduced in [23] and is based on the logic of minimal knowledge and negation as failure (MKNF) [21], provides a very general and flexible framework for combining DL ontologies and non-monotonic rules (see [23]). Second, [19], which is a variant of [23] based on the well-founded semantics [11] for logic programs, has a lower data complexity than the former – it is polynomial for polynomial DLs – and is amenable for applying top-down query procedures, such as SLG(O) [2], to answer queries based only on the information relevant for the query, and without computing the entire model – no doubt a crucial feature when dealing with large ontologies and huge amounts of data.
NoHR – the first Protégé plug-in to integrate non-monotonic rules and top-down queries – is implemented in a way that combines the capabilities of the DL reasoner ELK [17] (for EL+ ⊥) and a dedicated direct translation (for DL-LiteR) with the rule engine XSB Prolog, exhibiting the following additional features:

• rule editor within Protégé;
• possibility to define predicates with arbitrary arity;
• guaranteed termination of query answering;
• choice between one/many answers;
• robustness w.r.t. inconsistencies between the ontology and the rules;
• scalable fast interactive response times.

 

2 Preliminaries

We start with some preliminary notions to illustrate the kind of hybrid knowledge bases considered by NoHR. We begin with some notation on the description logics underlying the OWL 2 profiles, EL and QL, referring to [4] for a more general and thorough introduction to DLs. Then we present hybrid MKNF knowledge bases, followed by a basic description on how to perform query
answering.

2.1 Description Logics

The language of EL+ ⊥, a large fragment of EL++ [5], the DL underlying the tractable profile OWL 2 EL [22], is defined over countably infinite sets of concept names NC, role names NR, and individual names NI as shown in the upper part of Table 1.

Table 1: Syntax and semantics of EL+ ⊥.
Building on these, complex concepts are introduced in the middle part of Table 1, which, together with atomic concepts, form the set of concepts. We conveniently denote individuals by a and b, (atomic) roles by R and S, atomic concepts by A, and concepts by B, C and D. All expressions in the lower part of Table 1 are axioms. A concept equivalence C ≡ D is an abbreviation for C ⊑ D and D ⊑ C. Concept and role assertions are ABox axioms and all other axioms TBox axioms, and an ontology is a finite set of axioms.
The semantics of EL+ ⊥ is defined in terms of an interpretation I = (ΔI,⋅I) consisting of a non-empty domain ΔI and an interpretation function ⋅I. The latter is defined for (arbitrary) concepts, roles, and individuals as in Table 1. Moreover, an interpretation I satisfies an axiom α, written I|=α, if the corresponding condition in Table 1 holds. If I satisfies all axioms occurring in an ontology O, then I is a model of O, written I|=O. If O has at least one model, then it is called consistent, otherwise inconsistent. Also, O entails axiom α, written O|=α, if every model of O satisfies α. Classification requires to compute all concept inclusions between atomic concepts entailed by O.
In DL-LiteR one language of the DL-Lite family [7, 3] and underlying OWL 2 QL, complex concepts and roles can be formed according to the following grammar

B    → A∣∃Q    C    → B∣¬B    Q    → R∣R-    P    → Q∣¬Q
where, in addition to the already mentioned, R- is the inverse of the (atomic) role R.
A DL-LiteR TBox contains concept inclusions of the form B ⊑ C and role inclusions of the form Q ⊑ P, and a DL-LiteR ABox contains assertions of the form A(a) and R(a,b), with A, B, C, Q, P, and R defined as above.
The semantics of DL-LiteR is also based on interpretations I with the difference that I  assigns to each individual a a distinct element aˆI of ΔˆI and the following extensions to constructors not shown in Table 1 :

The notions of model (in-)consistency,and entailment coincide with those for EL+ ⊥.
EL+ ⊥ is tailored towards reasoning with large conceptual models, i.e., large TBoxes, while DL-LiteR focuses on answering queries over huge amount of data, i.e., large ABoxes. Standard reasoning tasks for both DLs are polynomial, in particular, classification for EL+ ⊥ is PTIME-complete, and query-answering for DL-LiteR even in AC0.

 

2.2 MKNF Knowledge Bases

MKNF knowledge bases (KBs) build on the logic of minimal knowledge and negation as failure (MKNF) [21]. Two main different semantics have been defined [23, 19], and we focus on the well-founded version [19], due to its lower computational complexity and amenability to top-down querying without computing the entire model. Here, we only point out important notions following [14], and refer to [19] and [2] for the details.
We start by recalling MKNF knowledge bases as presented in [2] to combine an ontology and a set of non-monotonic rules (similar to a normal logic program).

Definition 1. Let O be an ontology. A function-free first-order atom P(t1,…,tn) s.t. P occurs in O is called DL-atom; otherwise non-DL-atom. A rule r is of the form

H ←  A1,…,An,not B1,…,not Bm.        (1)
where the head of r, H, and all Ai with 1 ≤ i ≤ n and Bj with 1 ≤ j ≤ m in the body of r are atoms. A program P is a finite set of rules, and an MKNF knowledge base K is a pair (O,P). A rule r is DL-safe if all its variables occur in at least one non-DL-atom Ai with 1 ≤ i ≤ n, and K is DL-safe if all its rules are DL-safe.

DL-safety ensures decidability of reasoning with MKNF knowledge bases and can be achieved by introducing a new predicate o, adding o(i) to P for all constants i appearing in K and, for each rule r ∈P, adding o(X) for each variable X appearing in r to the body of r. Therefore, we only consider DL-safe MKNF knowledge bases.

Example 1. Consider an MKNF knowledge base for recommending vacation destinations taken from [23] (with a few modifications). We denote DL-atoms and constants with upper-case names and non-DL-atoms and variables with lower-case names.

PortCity(Barcelona)    OnSea(Barcelona,Mediterranean)
PortCity(Hamburg)    NonSeaSideCity(Hamburg)
RainyCity(Manchester)    Has(Manchester,AquaticsCenter)
Recreational(AquaticsCenter)
SeaSideCity    ⊑∃Has.Beach
Beach    ⊑ Recreational
∃Has.Recreational    ⊑ RecreationalCity
SeaSideCity(x)    ← PortCity(x),not NonSeaSideCity(x)
interestingCity(x)    ← RecreationalCity(x),not RainyCity(x)
hasOnSea(x)    ← OnSea(x,y)
false    ← SeaSideCity(x),not hasOnSea(x)
summerDestination(x)    ← interestingCity(x),OnSea(x,y)
This example shows that we can seamlessly express defaults and exceptions, such as every port city normally being a seaside city, integrity constraints, such as requiring to know for every seaside city on which sea it lies, and at the same time taxonomic/ontological knowledge including information over unknown individuals, such as a seaside city being recreational even if we do not know the specific name of the beach. Note that, unlike [23], the rule with head false is not a true integrity constraint in our case. Rather, whenever the keyword false would be derivable, we know that there is at least one seaside city for which we do not know on which sea it lies.
The semantics of MKNF knowledge bases K is usually given by a translation π into an MKNF formula π(K), i.e., a formula over first-order logic extended with two modal operators K and not. Namely, every rule of the form (1) is translated into a rule of the form KH ← KA1,…,KAn,not B1,…,not Bm, π(P) is the conjunction of the translations of its rules, and π(K) = Kπ(O) ∧π(P) where π(O) is the first-order translation of O. Reasoning with such MKNF formulas is then commonly achieved using a partition of modal atoms, i.e., all expressions of the form Kφ for each Kφ or not φ occurring in π(K). For [19], such a partition assigns true, false, or undefined to (modal) atoms, and can be effectively computed in polynomial time. If K is MKNF-consistent, then this partition does correspond to the unique model of K[19], and, like in [2], we call the partition the well-founded MKNF model Mwf(K). Here, K may indeed not be MKNF-consistent if the ontology alone is unsatisfiable, or by the combination of appropriate axioms in O and rules in P, e.g., axiom A ⊑¬B in O, and facts A(a) and B(a) in P. In the former case, we argue that the ontology alone should be consistent and be repaired if necessary before combining it with non-monotonic rules. Thus, we assume that O occurring in K is consistent, which does not truly constitute a restriction as we can always turn the ABox into rules without any effect on Mwf(K).

 

2.3 Querying in MKNF Knowledge Bases

In [2], a procedure, called SLG(O), is defined for querying MKNF knowledge bases under the well-founded MKNF semantics. This procedure extends SLG resolution with tabling [8] with an oracle to O that handles ground queries to the DL-part of K by returning (possibly empty) sets of atoms that, together with O and information already proven true, allows us to derive the queried atom. We refer to [2] for the full account of SLG(O), and only discuss central ideas here.
SLG(O) is based on creating top-down derivation trees with the aim of answering (DL-safe) conjunctive queries Q = q(X) ← A1,…,An,not B1,…,not Bm, where each variable in Q occurs in at least one non-DL atom in Q, and where X is the (possibly empty) set of requested variables appearing in the body. Query processing involving an oractle to the ontology is intuitively handled as described next.

Example 2. Recall  K in Ex. 1, and consider q = interestingCity(Manchester). We find a rule whose head unifies with q, and new queries RecreationalCity(Manchester) and not RainyCity(Manchester) are obtained. There is no rule whose head matches the former, but we can query the ontology and the answer is yes together with an empty set of atoms, i.e., RecreationalCity(Manchester) can be proven from  O alone. Now we handle not RainyCity(Manchester), so we query RainyCity(Manchester) which can also be proven by O alone. Consequently, not RainyCity(Manchester) fails, so q is false.
Now, consider q1 = interestingCity(Barcelona). We obtain again two new queries, q2 = RecreationalCity(Barcelona) and q3 = not RainyCity(Barcelona). In this case, q2 = RecreationalCity(Barcelona) cannot be proven from  O alone, but the oracle could return Has(Barcelona,X) and Recreational(X), which, if we would find a value for X, would allow us to derive q2. However, neither of the two atoms appear in a rule head in  P, so we will never be able to derive it from  P. In fact, the only proper answer the oracle may return is q4 = SeaSideCity(Barcelona). From the corresponding rule in  P we obtain two new queries q5 = PortCity(Barcelona) and q6 = not NonSeaSideCity(Barcelona). Then, q5 can be derived from O alone, and q6 succeeds, because NonSeaSideCity(Barcelona) fails. So q4 succeeds, and therefore also q2. Finally q3 succeeds since RainyCity(Barcelona) fails, so q1 is true.

 

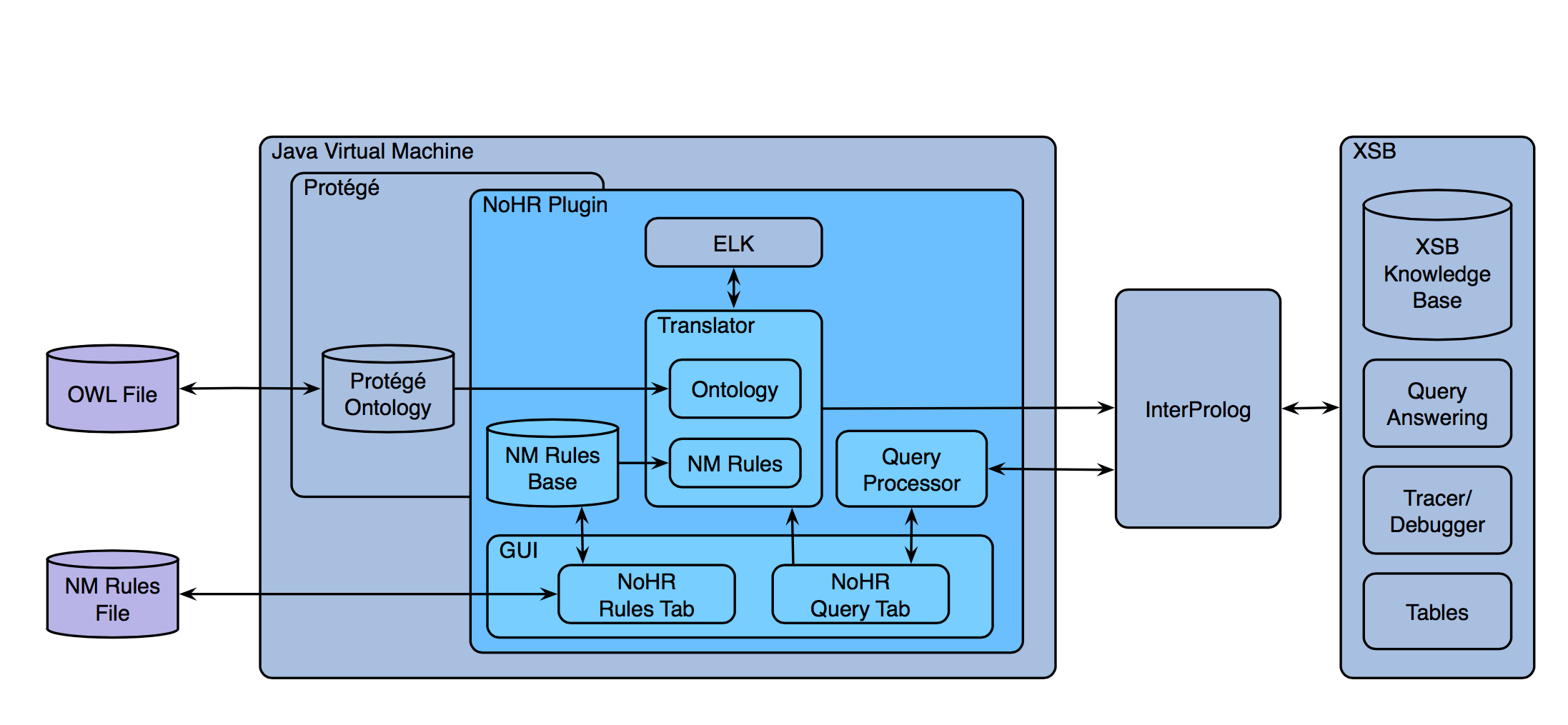
3 System Description

---

---

In this section, we briefly describe the architecture of the plug-in for Protégé as shown in Fig. 1 and discuss some features of the implementation and how querying is realized.
The input for the plug-in consists of an OWL file in the DL EL+ ⊥ or DL-LiteR as described in Sect. 2.1, which can be manipulated as usual in Protégé, and a rule file. For the latter, we provide a tab called NoHR Rules that allows us to load, save and edit rule files in a text panel following standard Prolog conventions.
The NoHR Query tab also allows for the visualization of the rules, but its main purpose is to provide an interface for querying the combined KB. Whenever the first query is posed by pushing “Execute”, a switch determines the profile of the ontology, upon which the translator is started. For EL+ ⊥, the ontology reasoner ELK [17], tailored for EL+ ⊥ and considerably faster than other reasoners when comparing classification time, is used to classify the ontology O. The inferred axioms together with O are translated discarding certain axioms which are irrelevant for answering ground queries. For DL-LiteR, a dedicated direct translation without prior classification is used, introducing some auxiliary predicates instead to compensate for the missing inferred axioms (see [14] and [9] for the respective details on both approaches). In both cases, the translation result is joined with the given non-monotonic rules in P, which is further transformed if inconsistency detection is required (in the presence of certain DL constructs in the ontology, such as DisjointWith axioms).
The result is used as input for the top-down query engine XSB Prolog which realizes the well-founded semantics for logic programs [11], and the transfer to XSB is realized via InterProlog,8 which is an open-source Java front-end allowing the communication between Java and a Prolog engine.
Next, the query is sent via InterProlog to XSB, and answers are returned to the query processor, which collects them and sets up a table showing for which variable substitutions we obtain true, undefined, or inconsistent valuations (or just shows the truth value for a ground query). XSB itself not only answers queries very efficiently in a top-down manner, with tabling, it also avoids infinite loops.
Once the query has been answered, the user may pose other queries, and the system will simply send them directly without any repeated preprocessing. If the user changes data in the ontology or in the rules, then the system offers the option to recompile, but always restricted to the part that actually changed.

 

4 Evaluation

---

---

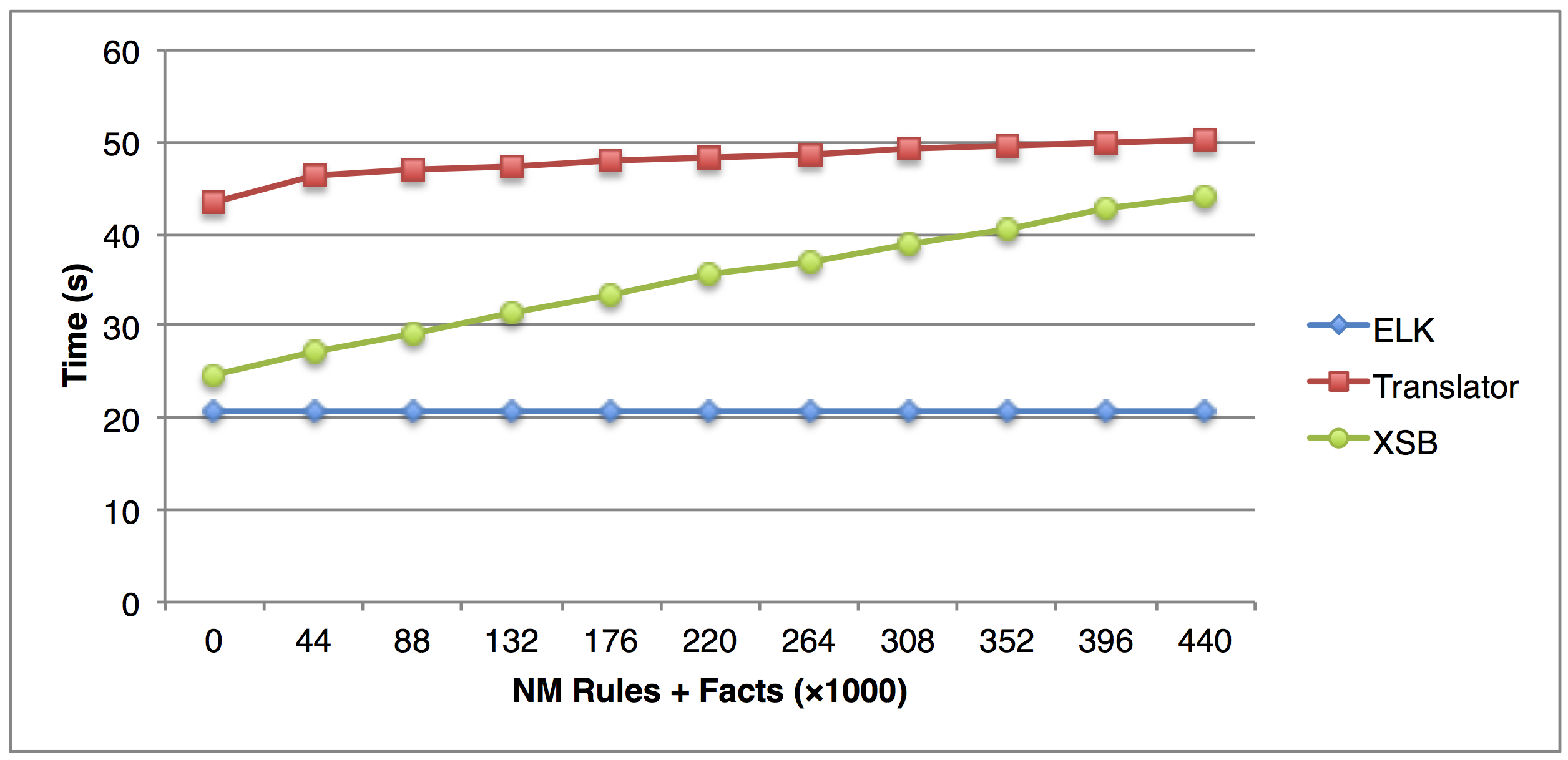
Tests on the EL+ ⊥ component alone already have shown that a) different EL ontologies can be preprocessed for querying in a short period of time (around one minute for SNOMED CT with over 300,000 concepts), b) adding rules increases the time of the translation only linearly, and c) querying time is in general neglectable, in comparison to a) and b) [14]. Fig. 2 visualizes the results from b) showing that the times for processing of files and ELK is basically independent of the number of added rules, and that the time of translator and XSB only grows linearly on the number of rules, with a small degree.
In subsequent tests on improved versions of both components (for EL+ ⊥ and DL-LiteR) [9], we have shown that i) our system scales reasonably well for OWL QL query answering without non-monotonic rules (only slowing down for memory-intensive cases), ii) preprocessing is even faster when compared to NoHR’s previous version using a classifier (for EL), which was already capable of preprocessing large ontologies in a short period of time, iii) querying scales well, even for over a million facts/assertions in the ABox, despite being slightly slower on average in comparison to EL, and iv) adding rules scales linearly for pre-processing and querying, even for an ontology with many negative inclusions (for DL-LiteR).
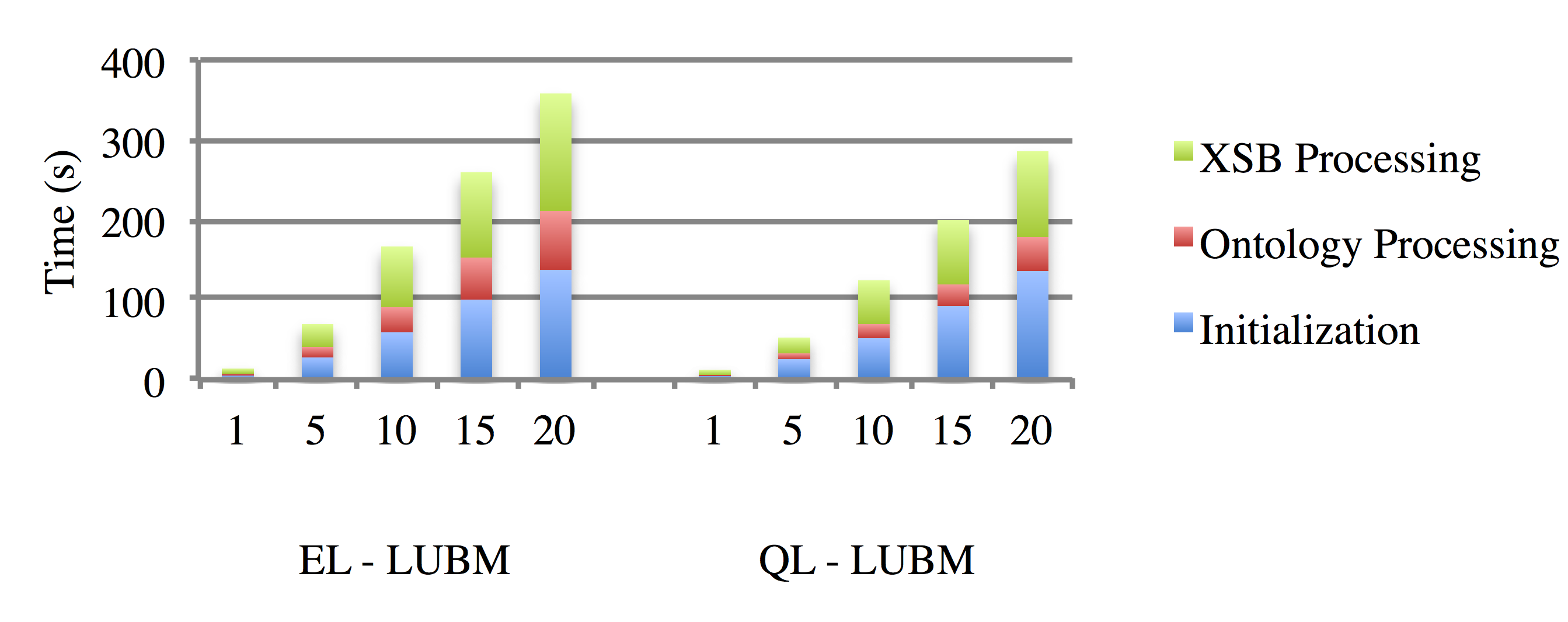
Fig. 3 shows the results for ii) where we considered LUBM [12], a standard benchmark for evaluating queries over a large data set, which also includes a given set of standard queries. We created instances of LUBMn with n = 1,5,10,15,20 using the provided generator, and a restricted version of LUBM which fits both OWL EL and QL (thus only rendering a few of the standard queries meaningless), with the number of assertions ranging from roughly 100,000 to over 2,700,000. Note that “Initialization” includes loading the ontology and for EL also classifying it, “Ontology Processing” includes the actual translation, and “XSB Processing” the writing of the rule file and loading it in XSB. We observe that QL is considerably faster, indeed up to 80s for LUBM20, which is to a considerable extent due to avoiding classification and a smaller rule file being created. This is compensated when querying as the DL-LiteR approach is slightly slower on average, and it thus seems that deciding which of the two forms of translation performs better depends on the kind (and number) of queries we pose.

 

---

---

5 Conclusions

The Protégé plugin NoHR – also distributed as an API – affords us the possibility to query knowledge bases composed of both an ontology in OWL 2 EL or QL and a set of non-monotonic rules, using a top-down reasoning approach, which means that only the part of the ontology and rules that is relevant for the query is actually evaluated. Its sound theoretical foundation together with the fast interactive response times make NoHR a truly one-of-a-kind reasoner.

Extending NoHR to the third profile – OWL 2 RL – seems an obvious next step, although developing an alternative for OWL 2 QL using the classifier integrated in ontop [20] or even the general reasoner Konclude [27], could shed more light on whether classification or direct translation fares better for proper OWL 2 QL ontologies. The efficiency of the latter reasoner also motivates looking into non-polynomial DLs, with possible influences from recent work on rewriting disjunctive datalog programs [15]. Adjusting NoHR to the paraconsistent semantics for MKNF knowledge bases of [16] would provide better support to the already observed paraconsistent behavior.

Acknowledgments.

We would like to acknowledge the valuable contribution of both Nuno Costa and Vadim Ivanov to the development of NoHR. This work was partially supported by Fundação para a Ciência e a Tecnologia (FCT) under strategic project PEst/UID/CEC/04516/2013, and grant SFRH/BPD/86970/2012 (M. Knorr).

References