MRCPSP-ENERGY, an energy-based scheduling problem

By
Daniel Morillo Torres, Federico Barber, and Miguel A. Salido
Instituto de Automática e Informática Industrial,
Universidad Politécnica de Valencia, Valencia, Spain

Abstract

The study of scheduling problems is one of the core areas in the planning and development of any project. Currently, researchers effort is addressed to optimize the task scheduling considering the energy consumption. In this paper a bi-objective MRCPSP (Multi-Mode Resource-Constrained Project Scheduling Problem)-ENERGY is proposed and transformed into a single-objective problem which takes into account both energy consumption and the makespan. Thus, the PSPLIB benchmark library is extended (called PSPLIB-ENERGY) to include energy consumption to each uni-modal RCPSP (Resource Constrained Project Scheduling Problem) instance, through a realistic mathematical model. This extension provides an alternative to the current trend of numerous researches about optimization and manufacturing field, which requires the inclusion of components to reduce the environmental impact in the decision making process. The PSPLIB-ENERGY is available at http://gps.webs.upv.es/psplib-energy/

Introduction

One of the main challenges in industry is to properly allocate available resources to tasks in order to optimize an objective function (usually makespan). The current trend is oriented towards obtaining efficient and sustainable solutions. Thus, the analysis and development of new methodologies for optimizing these problems including energy consumption have taken on greater importance in the last decades [1].

There are different strategies for energy optimization in manufacturing processes. These strategies can be classified into two levels: machine tool level and manufacturing system level [2]. The first level refers to improve the process taking into account the machine design, from a technological point of view [3, 4]. The second model emphasizes the energy optimization through the management and allocation of tasks and resources with the objective of minimizing energy requirements [5, 6]. Energy optimization at this level has a great importance and provides several improvement opportunities [7].

A Multi-Mode Resource Constrained Project Scheduling Problem (MRCPSP) is considered one of most important scheduling problems. These problems are well-known NP-hard problems, where relatively small instances are highly complex and it is not possible to find an optimal solution within a reasonable time.

This paper focuses on optimizing both makespan and energy efficiency in MRCPSP at manufacturing system level, by combining makespan and energy consumption as a single-objective function. Thus, MRCPSP-ENERGY is introduced, where the activities have different energy consumption to be executed at different rates. The objective is to minimize both makespan and energy consumption. Moreover, an extension of the well-known PSPLIB library (Project Scheduling Problem Library) [8] is proposed. This extension is made by associating an energy consumption to each activity in the traditional RCPSP library. This new library, called PSPLIB-ENERGY contains sets of instances for the MRCPSP-ENERGY.

MRCPSP-ENERGY: A MRCPSP extension for using efficiently energy

Formally, the standard MRCPSP can be defined as follows: A project consists of a set I of n activities I = {1,…,i,…,n}, a set B of K^ρ shared renewable resources B = {1,…,b,…K^ρ} available in R_b^ρ units, and a set K of K^ν shared non-renewable resources K = {1,…,k,…K^ν} available in R_k^ν units. Each activity i ∈ I holds m = {1,…,M} execution modes and a non-preemptive execution time d_im, requires r_imb^ρ units for every renewable resource b and r_imk^ν units for every non-renewable resource k. Generally, activities 1 and n are dummy activities that represent the start and the end of a project. Activities are subject to precedence constraints. Thus, an activity can not be started before all its predecessors activities are completed. The objective is to minimize the total duration of the project. The traditional mixed integer linear programming formulation can be found in [9].

Kolisch and Sprecher [8] proposed the PSPLIB library for assessing new developed methods that solve the RCPSP and MRCPSP by providing standard sets of trial cases. When the optimal solution is known, it can be calculated the average deviation regarding the optimal. Otherwise, an error is calculated based on the length of the critical path with the lowest execution time of each activity, called the deviation to LB0

This paper focuses on the MRCPSP considering only renewable resources to propose the MRCPSP-ENERGY. The analysis between energy consumption and makespan in scheduling is outlined below.

It is assumed that energy is a resource consumed by activities. As usually occurs in the machinery of materials, energy consumption of activities is independent of when they are scheduled [10]. Generally, as the energy consumption of an activity increases, its processing time decreases. Typical examples are lathes, milling machines, rolling stock, elevators, etc. [4, 11]. Hence, here it is assumed a similar energy behavior for MRCPSP activities. Finally, the total energy consumption of a project (CETP_w) can be calculated by using expression (1), where e_im is the energy consumption for an activity i executed in mode m.

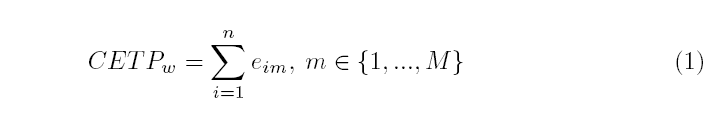
Project efficiency: optimization criterion in MRCPSP-ENERGY

In this section, an efficiency-based criterion is proposed. MRCPSP-ENERGY requires a bi-objective criterion that simultaneously minimizes both makespan (as the usual MRCPSP’s criterion) and energy consumption. In literature, when managing two objectives, a Pareto front is generated, but it is unsuitable to make a fair performance comparison since the operator must decide the weight to assign to each objective. The efficiency concept tries to give us a better solution for the whole system without influencing the significance of the objectives.

Generally, the concept of efficiency can be defined as the ratio between the energy supplied and the transformed energy delivered. For example, in manufacturing machine operations (like milling, turning, drilling, etc.), the theoretical efficiency of an electric motor is the conversion of electrical energy into mechanical energy. This is represented by expression (2), where η is the efficiency, P_mechanical represents the energy output from the motor shaft and P_electrical is the energy absorbed [12].

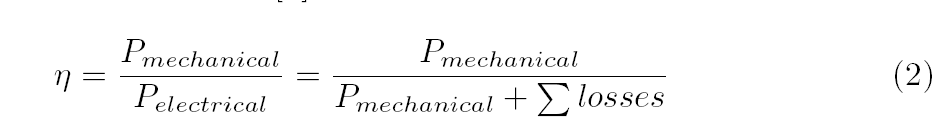
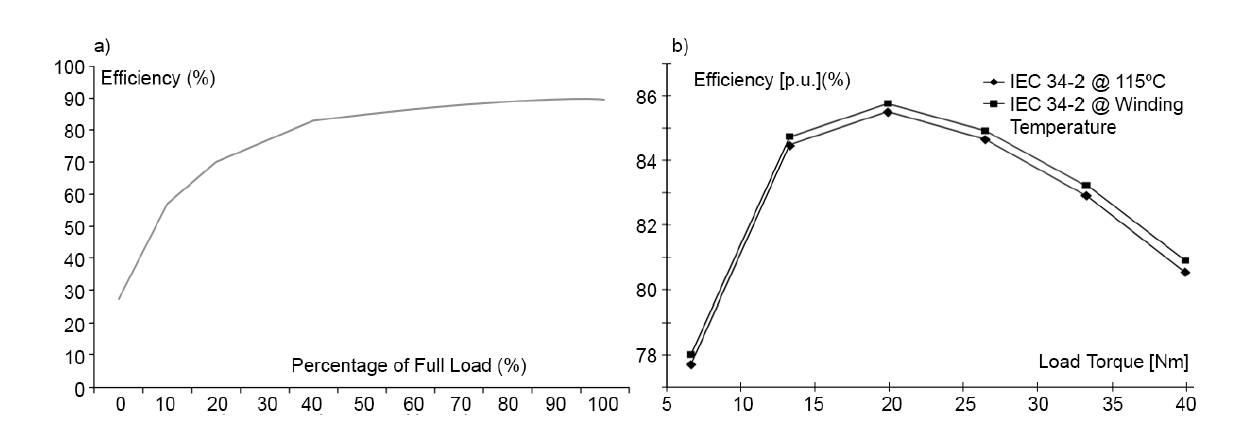
The expression (2) is a theoretical efficiency, which cannot reach a value 1, because of energy losses, mostly in the form of heat. The efficiency is characterized by an initial increasing curve until it reaches a horizontal asymptote (see Figure 1.a), some efficiency curves of different processes maintain the same trend. Theoretical behavior of efficiency is different in real practice, where efficiency decreases after reaching a maximum. For instance, Figure 1.b shows the efficiency performance of a real 4kw electric motor [12].

---

---

When energy is supplied to a motor, the output is mechanical energy. Meanwhile, the output for a project in which activities are carried out by machines or people, should be an duration affected by the amount of energy. The more energy, the less duration until the highest reduction is obtained, and then, more input might cause the machines work slower for overload, as it occurs in figure (1.b). The expression (3) describes this behavior for the duration d_i and the energy consumption e_i of an activity, but the range is not necessarily between 0 and 1.

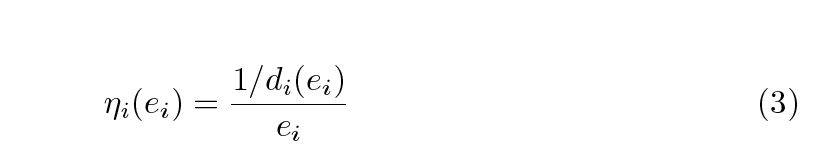
The previous concept can be extended to an entire project, expression (4). Nonetheless, as this relation is also out of 0 – 1 cannot be considered yet as an efficiency. If the optimal values of makespan and energy consumption were known, expression (4) could be standardized, but these values are unknown. Therefore, they are approximated by two lower bounds: emin_w and LB0min_w, respectively. The first is computed as (∑ _i=1ⁿe_i1) where e_i1 is the minimum energy consumption of activity i. The second is estimated by using the critical path method, considering the minimum processing time of each activity i within its m modes. In this way, an upper bound of the project performance CSR_w can be calculated to standardize expression (4). The expression (5) shows how to calculate CSR_w. It can be interpreted as the ideal efficiency of a project.

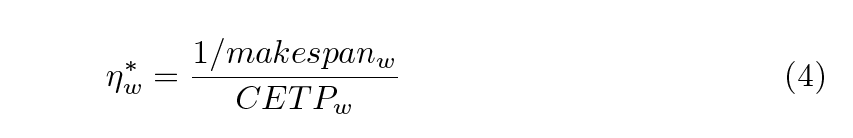
The expression (6) shows expression (4), now standardized. It is defined as the relative efficiency of the project w with respect to ideal.

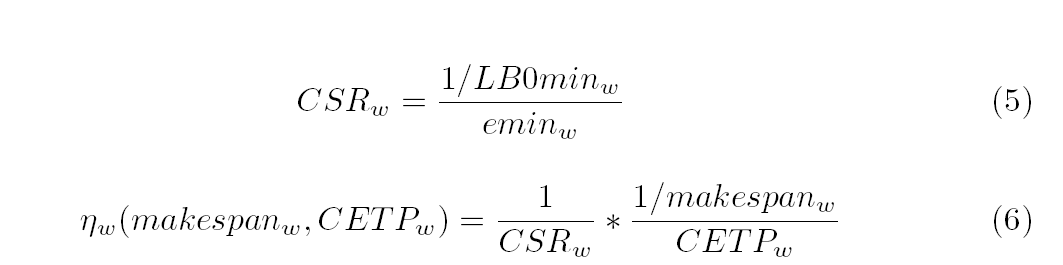
On the basis of the above concepts, MRCPSP-ENERGY can be defined as follows:

Definition 1: MRCPSP-ENERGY is a project that consists of a set of n activities I = {1,…,i,…,n}, a set B of K^ρ shared renewable resources B = {1,…b,…K^ρ}, and there is an available amount R_b^ρ of every renewable resource. Each activity i holds m = {1,…,M} execution modes and a non-preemptive execution time d_im, requires a total of r_ib renewable resource of type b and an amount of energy e_im for its realization. Activities are subject to precedence constraints, which indicate that each activity can not be started before all its predecessor activities are completed. The different energy consumptions for an activity give rise to different execution modes. Thus, MRCPSP-ENERGY is similar to a RCPSP where the activities have different execution modes, associated to different energy consumptions.

The main differences with respect to a traditional MRCPSP are: (1) modes depend entirely on energy consumption e_im and the relation between energy consumption and processing time is inverse and (2) the objective is to maximize the project efficiency, which means to minimize both energy consumption and makespan.

The formal mathematical model of the MRCPSP-ENERGY maintains the same constraints than MRCPSP [9] without the non-renewable resources constraints and the objective function is reformulated according to the expression (7).

PSPLIB-ENERGY: An extension of PSPLIB library

In this section the PSPLIB-ENERGY library is proposed. It complements the PSPLIB with different levels of energy consumptions and processing times associated to each activity. This extension aims to evaluate search methods for optimizing the MRCPSP-ENERGY, taking into account both makespan and energy consumption, by using the proposed efficiency-based criterion.

Model proposed for energy consumption

For expanding the PSPLIB library it is necessary that the values of energy consumption for activities and their corresponding processing times to be consistent with the behavior of real machines. For this purpose, a standard value of energy consumption e_i and a processing time d_i for each activity is assigned a priori. Afterward, a mathematical model relates the standard values with every mode of an activity to compute its value of energy consumption and processing time.

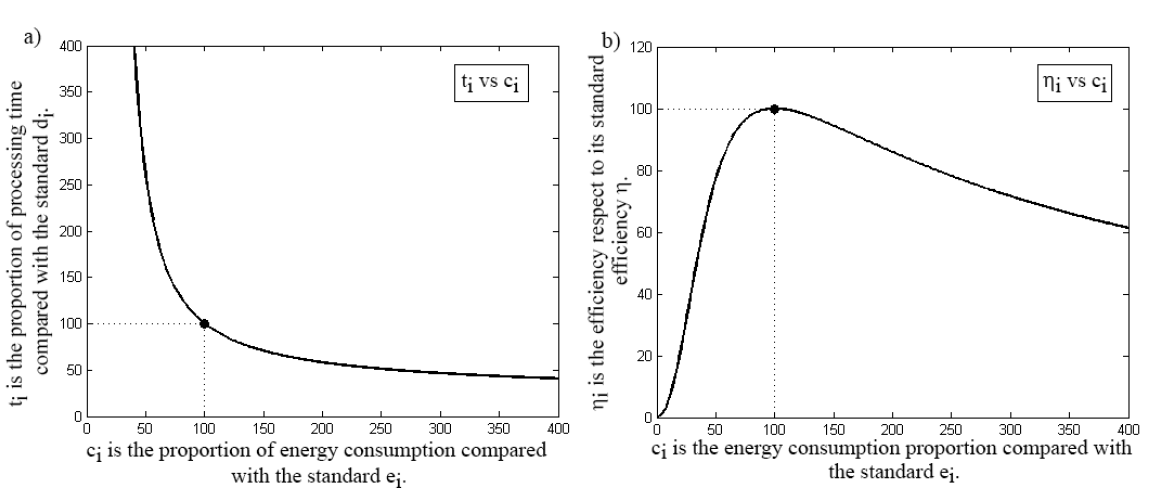
In machining, there is not a global mathematical model that describe all behaviors of energy consumptions in machine tools. This is due to the fact that energy consumption behavior depends on several technical factors. Nevertheless, the behavior is quite similar in most machines. The relationship between energy consumption and processing time of machining has a decreasing trend [10]. In this way, it proposes the expression (8), where t_i(c_i) is the proportion of processing time compared with the standard duration of the activity i, and c_i is the proportion of energy consumption compared with the standard consumption of the activity i. The expression (8) has a decreasing trend in a similar way to that of the energetic behavior on machine tools. This function represents an approximation of the efficiency model proposed in the previous section. The values of the constants A₁ = 4.0704 and A₂ = 2.5093 center the function in c_i = 1(100%) and t_i = 1(100%), representing the standard of the energy consumption and the processing time, respectively. As example, a value of c_i = 1,6(160%) represents a consumption of 60% of additional energy for activity i, and an obtained value t_i = 0,67(67%) represents a decrease of 33% in the processing time of the activity i. Figure 2-a) shows the graph of the expression (8).

 

 

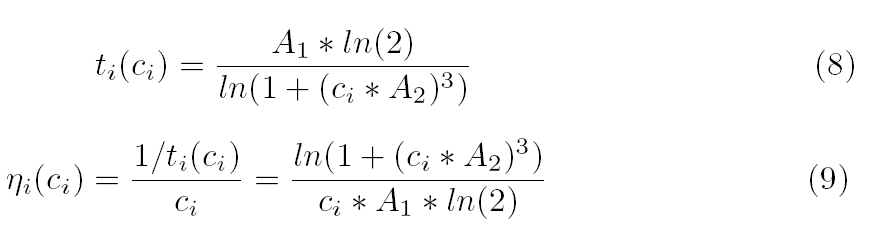
As a result of previous energy-time model, expression η_i(c_i) (9) is defined as the relative efficiency of the activity i depending on c_i. This expression can be interpreted as the efficiency percentage of the activity i respect to its efficiency, when both standard energy and standard processing time are used. For instance, a η_i(c_i) = 130% indicates that, given a proportion of energy consumption c_i, an efficiency of 30% higher than the standard is obtained. Figure 2-b) shows the relative efficiency expression (9). It is important to note how the trend of the curve is similar to the real efficiency shown in figure 1.

 

---

---

Energy extension for PSPLIB

To extend the PSPLIB to PSPLIB-ENERGY, it includes energy consumption and processing time to each activity in the uni-modal RCPSP instances, through the mathematical model described above (expression 8). Thus, the four problems sets: j30,j60j90 and j120 were created. With 30, 60, 90, and 120 activities, respectively. Each of them with 480 instances, except the last one that have 600 instances. The values of the standard efficiency of each instance are available on the PSPLIB-ENERGY library.

Without loss of generality, three specific values for energy consumption e_im were taken. Thus, three modes are defined. The first mode (c_i1 = 0.8) corresponds to a decrease of 20% in the energy consumption related to the standard value e_i2. The second mode (c_i2 = 1) has the standard value of energy consumption e_i^std = e_i2 which corresponds to the standard duration d_i^std = d_i2 provided by the original PSPLIB library. The third mode (c_i1 = 1.2) corresponds to an increase of 20% in energy consumption related to the standard value e_i2.

The corresponding values of processing time (d_im) and energy consumptions (e_im) can be calculated using expressions (10) and (11), respectively. The values of t_i(c_im) are calculated using expression (8).

The values of e_i^sdt are defined by assigning to each activity on the PSPLIB-ENERGY library a random consumption value that range in [1,10]. This ranges of values was proposed considering the same intervals used for the original parameters on the PSPLIB library. As all parameter values in the PSPLIB library are integers, the values of the parameters for PSPLIB-ENERGY library are also integers.

For the evaluation of further developed techniques using the PSPLIB-ENERGY library, the criteria is to maximize the relative efficiency presented in expression (6). This expression takes into account both makespan_w and the energy consumption CETP_w (expression 1) in a single-objective.

To calculate the average value η for the problems of the sets j30, j60, j90 or j120 on PSPLIB-ENERGY, the expression (12) is defined, where nP is the number of evaluated projects.

An example of a MRCPSP-ENERGY instance

In this section, an example of a small MRCPSP-ENERGY instance is presented. This instance consists of n = 8 activities and B = 3 renewable resources. Figure 3 shows the energy consumption (e_im), the processing time (d_im) and the resource usage (r_imb^ρ).

---

---

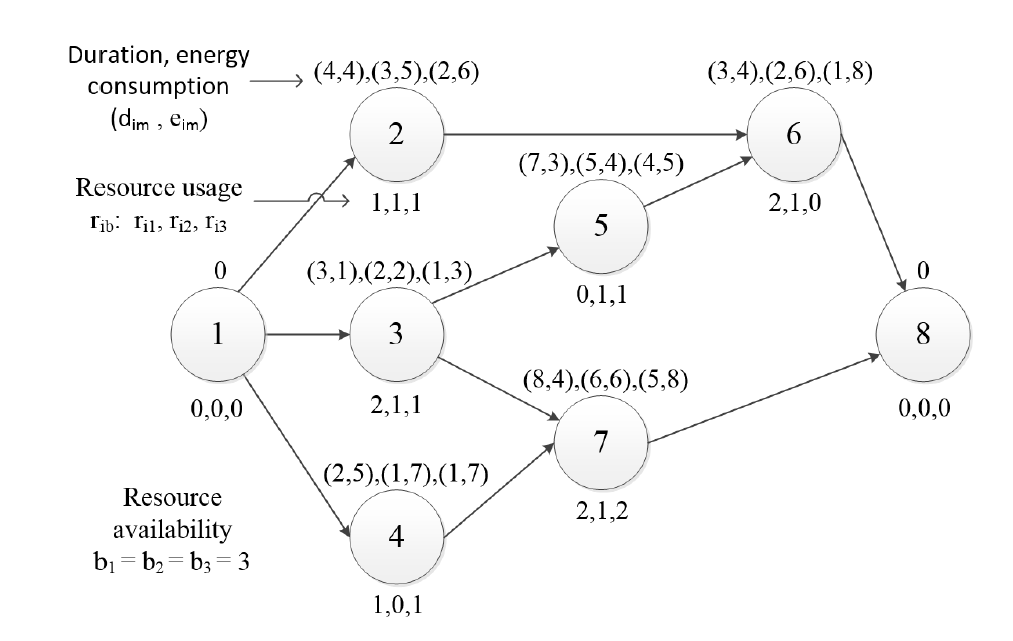
Figure 4 shows three Gantt charts of three solutions for the given instance. Figure 4.a shows an optimal solution when the problem only uses a proportion of energy consumption c_i = 100%. Figure 4.b and Figure 4.c represent two solutions using different energy consumption, and consequently, different processing times.

---

---

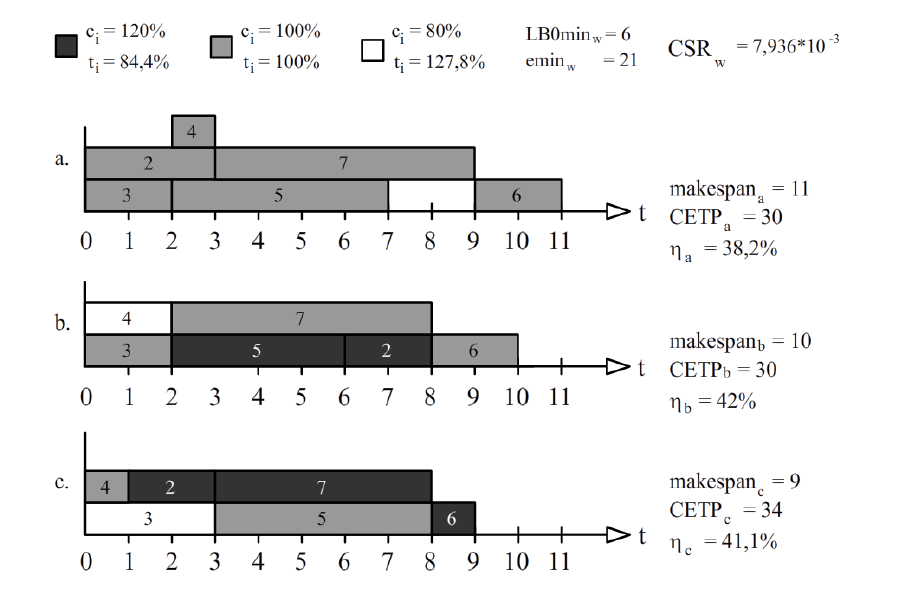
To calculate the efficiency η_w of each solution, the values LB0_w = 6 and emin_w = 21 were calculated from Figure 3. Figure 4 shows the upper level of project performance CSR_w, the value of the total project duration makespan_w, the total energy consumption of the project CETP_w and the value of the evaluation criterion η_w for three different solutions.

The solution (a) has the lowest value of efficiency η_a = 38,2%. The lowest makespan is achieved in solution (c). However it has the highest energy consumption so its efficiency is η_c = 41,1% and it is considered better than solution (a). The solution (b) maintains the same energy consumption than solution (a) but improves in makespan so it achieves the highest value of the relative efficiency of the project η_b = 42%. Thus, the solution (b) is considered to be the best solution of the three ones.

It is noteworthy that the efficiency values are relatively low in all cases (close to 40%), because they are compared with the ideal value of the upper bound of project performance CSR_w.

Conclusions

Currently, many researches follow the strong trend to develop models that include an energy component for obtaining sustainable solution to scheduling problems. As a result, it is necessary to develop new libraries to evaluate the behavior of further developed heuristics.

A single-objective MRCPSP efficiency-based criterion has been proposed. It is called MRCPSP-ENERGY, which includes the energy consumption in a scheduling problem. The proposed approach consists in maximizing the relative project efficiency. This is carried out by minimizing simultaneously the makespan and the energetic consumption. The efficiency concept tries to find the best solution for the system as a whole and to avoid the generation of the Pareto front. Whereas the activities can be done with different modes, each with different energy consumption, the obtained results show that can be obtained more energy efficient solutions.

Therefore, the PSPLIB-ENERGY library is proposed. This library introduces a new set of test cases where new computational methods can be tested for efficient resolution of MRCPSP with the combined objectives of energy efficiency and makespan. PSPLIB-ENERGY is supported by a proposed model of energy consumption, which is consistent with surveys reported in the academic literature about energy consumption for machines. It has been developed keeping the same format than PSPLIB library, with four sets of problems (j30, j60, j90 and j120), every of those with 480 problems, except the set j120, with 600 instances. This library is available at http://gps.webs.upv.es/psplib-energy/.

References