Bound Founded Answer Set Programming

By
Rehan Abdul Aziz
Geoffrey Chu
Peter James Stuckey
University of Melbourne and NICTA

PDF Version

Bound Founded Answer Set Programming (BFASP) [2] is a formal system that generalizes two well-known declarative programming paradigms Constraint Programming [7] and Answer Set Programming [6]. Two important features of combinatorial solvers are the ability to reason over finite integer domains and foundedness (which, we hope, will become clearer later in the article). CP systems support the first but lack the second, whereas while ASP systems do support foundedness over Boolean variables, they are inherently propositional (Boolean), and are therefore, handicapped in reasoning over integer variables efficiently. There have been attempts to combine the strengths of ASP and CP, but almost all of them merely put the two systems together, i.e., the combination supports integer variables and foundedness only for Boolean variables. BFASP is a more complete integration that actually defines what foundedness means for numeric quantities. Let us motivate BFASP with the help of an example from this domain.

 

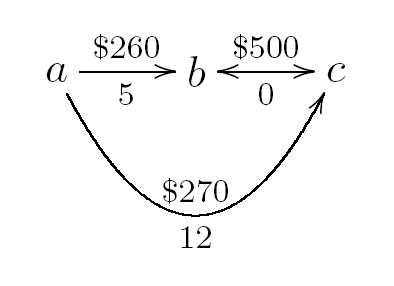
Figure 1: A simple potential road network with distances, and costs to build road segments.

The directed graph in the Figure 1 is a potential road network where the edges represent one-way roads. Moreover, each edge has a distance and a cost (in thousands of dollars) associated with it, which are written below and on top of the edge respectively. Our goal is to minimize the sum of shortest paths from a to b and a to c (Realistically speaking, there are not many one-way roads. We have simplied our example to keep the number of rules short. This simplication is also inconsequential since we are only interested in the shortest paths from a, which means that we omit all arcs entering a).

The sites b and c have a negligible physical distance if we build the expensive two-way bridge between them (e.g. they are two sites on the opposite sides of a narrow river). We are also constrained by our available budget, which is $550. In this simple example, the optimal solution is to build the roads ab and ac with the total cost of 530. If we build the bridge between b and c, then we have no money to build any other road and as a result, sitesb and c become unreachable from a. Let us now model this problem in BFASP and show why it cannot be efficiently encoded in any competing formalism.

Let build_xy represent the decision whether we build the road from x to y and let sp_xy represent the length of shortest path from x to y. For every edge (u,v) in the graph, and any node x, it is easy to see that if the edge is built, then sp_xv is at most sp_xu plus the distance along the edge. Furthermore, the shortest path from a node to itself is at most 0. Let Nodes, Edges be the set of nodes and edges, and let d_uv represent the distance for the edge (u,v). These above ideas can be used as rules to define shortest paths in BFASP as follows:

∀x ∈ Nodes :                 sp_xx ≤ 0

∀x ∈ Nodes,(u,v) ∈ Edges : sp_xv ≤ sp_xu +d_uv ← build_uv

We can instantiate above rules for our example to get the following ground rules:

sp_aa ≤ 0            sp_bb ≤ 0            sp_cc ≤ 0

sp_ab ≤ sp_aa +5 ← build_ab  sp_ac ≤ sp_ab ← build_bc sp_bc ≤ sp_bb ← build_bc

sp_ac ≤ spaa + 12 ← build_ac  sp_ab ≤ sp_ac ← build_bc sp_cb ≤ sp_cc ← build_bc

We ignored some ground rules like sp_bb ≤ sp_ba + 5 ← build_ab since they are subsumed by sp_bb ≤ 0 etc.

We also ignored some rules like sp_cb ≤ sp_ca + 5 ← build_ab since c can never reach a etc. Our budget constraint can be formally written as:

260 ×build_ab + 270 × build_ac + 500× build_bc ≤ 550

To the best of our knowledge, shortest path definitions like the one above, cannot be feasibly modeled in ASP. One way to do so is to propositionalize or ground the shortest path upper bounds for each value in the integer domain and add further ASP rules to ensure that the upper bound variables collectively correctly encode the integer domain. This, unsurprisingly, becomes impractical for large distances. We have explained this in detail in [1, 2]. (An attempt to model the problem above in ASP can be found at: http://people.eng.unimelb.edu.au/pstuckey/bound_founded/encodings/road.gringo and some instances can be downloaded from: http://people.eng.unimelb.edu.au/pstuckey/bound_founded/road.zip)

Now, imagine if we pass the above model to a CP (or a CASP) solver; no matter what the values of build variables are, as long as the budget constraint is satisfied, all shortest path variables can be set to 0 and it is still a valid model. This is, of course, not correct. The reason is that a CP solver treats the shortest path variables as regular integer variables, whereas the semantics we wish to give these variables is different. In absence of any rule, we require a shortest path variable to be ∞. Furthermore, if there is any rule, then it can justifiably take on a smaller value as given by the LHS of that rule. In other words, its upper bound needs to be founded by some rule. For this reason, we refer to the type of variables like sp as upper-bound founded in BFASP. Similarly, there can be lower-bound founded variables which are by default equal to -∞ and further rules justify a higher value. With this generalization, ASP variables are simply lower-bound founded Boolean variables. Another rich feature of BFASP is that as opposed to syntactically limited ASP rules which are simple logical implications (with certain limited extensions like weight rules etc.), rules in BFASP can be formed using a variety of primitive rules recursively. We have discussed the language aspects of BFASP along with how to ground first-order rules efficiently in [3].

We might think that it is possible to model the shortest path rules in CP using standard variables only and setting shortest path variables equal to the minimum value allowed by their rules as follows: (here M is a sufficiently large number, used to model ∞, and in slight abuse of notation, we access build variables as 0-1 integer variables):

∀x ∈ Nodes :   spxx = 0

∀x ∈ Nodes : sp_xv = min {M,(sp_xu + d_uv)* build_uv +M  * (1 – build_uv) : (u,v) ∈ Edges}

Let us see what happens in our example if the CP solver decides to build only the bridge, and not any other road, i.e., build_ab = build_ac = false and build_bc = true. We get the following simplified expressions:

sp_aa = 0 sp_bb = 0           sp_cc = 0      sp_ab = min{M, sp_ac}          sp_ac = min{M, sp_ab}

which means any assignment that satisfies the constraint sp_ab = sp_ac is a valid solution, which is wrong. This is because in BFASP semantics, which extend the stable model semantics used in ASP, two or more variables cannot simultaneously justify bounds on each other without having any independent justification. For example, if we have two ASP variables i and j, and only two rules i ← j, and j ← i, then they cannot be set to true since the only way to justify that value relies on circular reasoning. In fact, avoiding this kind of circular derivation of bounds is at the heart of BFASP implementation. The main idea of the algorithm, which generalizes a similar algorithm for founded Booleans in ASP, is to keep a justification graph, defined over bounds of founded variables, that records for each bound, other bounds that were used to derive it. The algorithm ensures that this justification graph is acyclic at all times, which guarantees that there is no circular derivation. Our experiments have shown that this algorithm for implementing BFASP allows us to solve a range of problems more efficiently than ASP, CP, or Constraint ASP (CASP) [5, 4] systems.

References