Semantics at Scale: When Distributional Semantics meets Logic Programming

Abstract

Distributional semantic models (DSMs) are semantic models which are automatically built from co-occurrence patterns in unstructured text. These semantic models trade representation structure for volume of semantic and commonsense knowledge, and provide effective large-scale semantic models which can be used to complement logical knowledge bases. DSMs can be used to inject large scale commonsense knowledge into logical knowledge bases (KBs), supporting semantic approximations between queries and KBs and approximative reasoning over incomplete knowledge bases. This article provides an informal overview of distributional semantic models and their applications to logic programming, defining the basic steps on how you can build your first distributional-logic program.

PDF Version

1 On querying and commonsense knowledge

Suppose we want to query a knowledge base KB created by a third party. In general we may have an idea on the type of content present in the dataset, but we may not know exactly which terms are used to describe constants and predicates.

Suppose we decide to try our luck and we issue the following query over the KB (‘Is the father-in-law of the daughter of Bill Clinton a politician?’):

?- daughter_of(X,bill_clinton), politician(Y),father_inlaw(Y,X).

The KB contains the following facts and rules:

child_of(chelsea_clinton,bill_clinton).
child_of(marc_mezvinsky,edward_mezvinsky).
child_of(hilary_clinton,hugh_rodman).
spouse(chelsea_clinton,marc_mezvinsky).
spouse(bill_clinton,hilary_clinton).
is_a_congressman(edward_mezvinsky).
father_in_law(A,B) ← spouse(B,C), child_of(C,A).

The query cannot be answered since daughter_of and politician are not defined predicates in the knowledge base, despite the fact that the information is expressed in the knowledge base.

One practical issue that is present when querying logical knowledge bases is the fact that users need to have an a priori understanding of the ‘schema’ behind the KB. The cost associated with the ‘a priori interpretation’ of the knowledge base from the data consumer side, strongly impacts the interaction with logical knowledge bases. As the knowledge base grows in size, the associated KB interpretation effort associated with the query process may become prohibitive.

A possible solution for this problem would require the KB designer to anticipate possible user queries and encode the associated commonsense and semantic knowledge as facts and rules in the KB (for example, that child_of(A,B) ← daughter_of(A,B)). However, the associated scalability problems which emerge of representing large-scale logic KBs (such as knowledge acquisition and consistency) makes this solution unpractical.

2 Building large-scale semantic and commonsense knowledge

Supporting the type of approximations in the previous example depends on the structured representation of large-scale semantic and commonsense knowledge. However, the construction of a large-scale structured commonsense knowledge infrastructure has been a major challenge for different projects (such as Cyc [9]) and whole research communities (such as the Semantic Web). At the center of the challenge is an intrinsic trade-off between an expressive structured semantic (formal) representation model and the effort necessary to materialize a knowledge base under a formal representation framework. We refer to this as the expressivity-acquisition trade-off.

Distributional semantics approaches have been proposed to address this trade-off by simplifying the semantic representation requirements. This simplification trades data structure for data acquisition scale and supports the construction of comprehensive semantic and commonsense models from information extracted from unstructured texts. Most of the wealth of information available on the Web is in the form of natural language: the ability to harvest semantic and commonsense knowledge embedded in Web texts, brings an enormous opportunity for the construction of comprehensive semantic and commonsense models.

Distributional semantic models brings principled, effective, easy-to-build and easy-to-use approaches which can be used to inject semantic flexibility and large-scale commonsense knowledge into logic programs and structured knowledge bases in general. The ability of performing semantic approximations supported by vast amounts of commonsense data, brings the possibility of building semantically flexible logic programs.

This article introduces the core elements of distributional semantic models, and also provides the tools to build your first distributional semantics logic program.

3 What is distributional semantics?

Distributional semantics is based on the distributional hypothesis which states that: “Words occurring in similar (linguistic) contexts tend to be semantically similar”  [8]. For example in the sentence below:

“They poured the wine into the klsl and drank among friends in the meal.”

Part of the meaning of the word klsl can be inferred by its neighboring words (its linguistic context). The application of this principle over large text collections supports the construction of semantic models based on co-occurrence patterns over unstructured text.

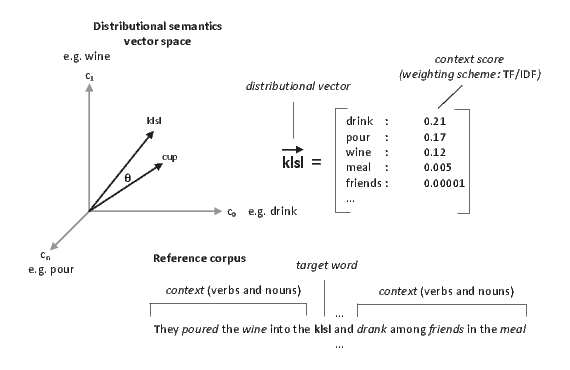
The representation model behind distributional semantics is based on a vector space model, where the meaning of a word is represented as a weighted vector of a set of context (linguistic) features (which defines the the dimensions of the vector space). The context features co-occurring with a target word (the word that we are creating the associated semantic representation) serve as surrogate for its meaning representation. In our example, the context is defined as the verbs and nouns present in the same sentence of the target word (Figure 1).

“They poured the wine into the klsl and drank among friends in the meal.”

As other sentences in the corpora are analyzed to build the distributional semantic vector for the word, discrimination measures based on the number of co-occurrences for each context feature can be used to weight-up contexts with stronger associational patterns (e.g. drink) and weight-down contexts which are weakly associated with the meaning of the word (e.g. friends). Term-frequency / inverse document frequency – TF/IDF  [7] is an example of a weighting scheme used in distributional semantic models. Figure 1 depicts the vector for the example sentence in the reference corpus.

4 Semantic approximation everywhere (quick and not that dirty)

The vector representation model provides a simplified geometric representation of meaning which encodes the semantic associations between words. Once a distributional semantic model (DSM) is built for a domain, the geometric proximity between two vectors in the distributional vector space can be computed using measures such as cosine similarity or euclidean distance  [7]. Under the DSM, the geometric proximity between two vectors is proportional to the semantic similarity and relatedness between the two words (Figure 1). The computation of semantic similarity and relatedness can be used to compute semantic approximations of elements in the query and in the KB, using the distributional semantic representation extracted from the corpora (i.e. vector proximity/similarity → semantic similarity/relatedness → semantic approximation).

The simplicity of vector spaces as a semantic representation model, facilitates both the acquisition of semantic and commonsense knowledge from unstructured data and also the computation of semantic approximations. The semantic approximation process is simplified from a deductive reasoning based process over a potentially large manually curated commonsense KB (traditional approach) to an approach based on the computation of vector similarity operations over a distributional vector space. This provides an approach which scales better from the knowledge acquisition perspective at the expense of some level of inaccuracy in the semantic approximation process. From an accuracy perspective, there is empirical support on the accuracy of distributional semantics as a semantic approximation mechanism in the literature  [7, 1].

5 Predicates in Space: Programming with distributional semantics

One of the most promising applications of DSMs is to use them to inject large-scale semantic & commonsense knowledge into structured knowledge bases/logic programs. The introduction of semantic and commonsense knowledge into structured KBs supports semantic approximations of predicates, constants, facts and rules, addressing challenges which are dependent on the construction of large-scale semantic models such as flexible querying, approximative reasoning, entity consolidation/KB integration, among others.

The process of extending a KB with an associated distributional semantic model consists in creating the distributional vectors for the natural language labels of all the predicates and constants in the KB. For example, for the predicate ‘spouse(X,Y)’, the extension of the predicate in the KB is extended with the associated distributional vector of the term ‘spouse’ which captures its associations with other terms in the corpora and outside the KB (e.g. ‘wife’, ‘husband’, ‘married to’, ‘family’, etc). This allows the KB to cope with queries which were not anticipated by the KB designer. For a KB containing the fact spouse(bill_clinton,hillary_clinton) a query such as wife(bill_clinton,x) could be resolved using the distributional semantics vector representation.

For a hybrid distributional-logic program, all program entities (logic predicates and constants) are embedded into a distributional vector space, and the KB has an associated distributional geometric interpretation under a distributional semantic model. The distributional representation of the KB entities’ supports semantic approximations based on the DSM, which can be used to introduce semantic flexibility in processes such as querying, reasoning or KB integration.

6 Do-it-yourself: ‘Hello Distributional World!’

Our first distributional-logic program uses a distributional semantic model as a commonsense knowledge base to do semantic approximations in the predicates of the example KB introduced in Section 1.

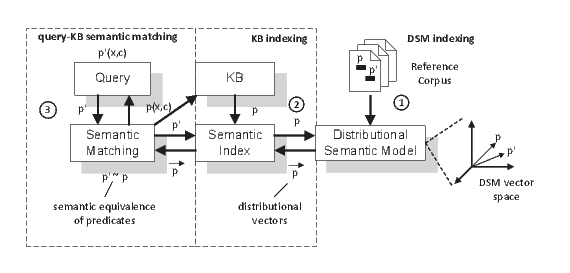
Figure 2 shows the components involved in the process of building a distributional semantics logic program. In order to support a flexible semantic approximation, the KB is complemented with a distributional index. The distributional index is automatically built from the knowledge base of facts and rules, and aligns the semantics of the natural language descriptors (labels) associated with predicates, to their distributional representation. In our example program, the distributional index is built using a supporting distributional semantic model, which builds the word vector representation using semantic and commonsense knowledge embedded in unstructured text. The implementation of a distributional index inherits data structures available in information retrieval (optimization strategies in the creation of inverted indexes) which aims at minimizing the complexity associated with the computation of the vector similarity. This example uses the EasyESA framework  [5] as a distributional semantics framework, which builds a distributional semantic model out of the knowledge present in Wikipedia.

The distributional index contains the vector representations for the logic program predicates. The distributional index supports the computation of a distributional semantic relatedness measure (i.e. distance measure between the distributional vectors) between the query terms and a subset of the predicates represented in the knowledge base, which returns a ranked list of predicates in the KB related to the query predicates. Scores above a threshold are considered to be semantically similar (Figure 3). The semantic approximation supports the query-KB predicate substitutions:

daughter_of ~ child_of and is_a_congressman ~ politician

With the semantic approximation, the answer (X = chelsea_clinton,  Y = edward_mezvinsky) can be computed.

The process is transparent to the user: the semantic and commonsense knowledge used in the semantic approximation is automatically extracted from the text corpora and used to build the distributional semantic index. However, the semantic approximation process is dependent on a heuristics which minimizes the impact of the semantic uncertainty (ambiguity, vagueness) associated with the query-KB alignment. The heuristics defines a query-KB alignment which provides a strong context definition for the query-KB semantic approximation. This strong query-KB alignment is called a semantic pivot. The use of semantic pivots supports the reduction of the semantic matching space, computing only approximations which are associated to the query context. The details on the definition of these heuristic models for the semantic pivot selection can be found in  [1].

In the previous example we focused on the description of an example query-KB semantic approximation. This model can be generalized into an approximate reasoning model over incomplete knowledge bases. However, the coverage of this aspect is beyond the scope of this article. Detailed references of this generalization can be found in  [2, 1, 3] .

Besides semantic approximation between queries and KBs and approximate reasoning over incomplete KBs, the creation of hybrid distributional-logical models can be used to support the discovery of similarity patterns in KBs in tasks such as entity reconciliation (where constants and predicates in different KBs can be automatically integrated) and in knowledge discovery applications such as relation/link discovery (discovering implicit associations between entities in the KB)  [4].

7 What does distributional semantics bring to the table?

In a nutshell, the application of distributional semantics to logic programs provides a knowledge representation framework with distinctive features from both a theoretical and a practical perspective. These features are summarized below:

• Semantics for a heterogeneous world: DSMs can be built using unstructured, inconsistent and semantically heterogeneous data, providing semantic models which can be built out of commodity textual data.
• Large-scale automatic semantic acquisition: the simplicity of the semantic representation model behind distributional semantics (vector-based representation) facilitates the acquisition of large-scale semantic and commonsense knowledge, automatically from text. As the scale of the reference corpora increases, more comprehensive models (multi-domain and multi-lingual) can be built.
• Simplicity of use: DSM are easy-to-build, easy-to-scale and easy-to-use. There are already infrastructures such as EasyESA [5] and S-Space [6] which facilitate the construction of large-scale DSMs.

Distributional semantics enables the introduction of semantic flexibility into rigid knowledge representation frameworks, providing a complementary semantic layer to logic programs, relational data and Semantic Web data. Hybrid distributional-logical representation frameworks bring the promise of providing an approach to cope with KB incompleteness, which can impact important recurrent tasks for users and applications such as semantically flexible querying, reasoning and KB integration.

References