Divide and Conquer (Where Has All the Good Democracy Gone?)

Year 2014, country of Batalia. The power of Silvestro Tomboloni, who has been prime minister several times over the last twenty years, seems to be irreversibly declining. A new young leader, Matthew Fonzy is taking over. A large majority of the electors is supporting the young bright Matthew, who is planning to completely renovate the organisation of the country.

Tomboloni seems to be out of the game, of 48,828,125 electors only 200,000, a very small percentage (0.36%), are supporting his party.

Suddendly … an idea! Among the many changes prime minister Fonzy has in mind, there is a complete reform of the electoral system. The new system for electing prime minister is very dynamic, in line with his youngish attitude.

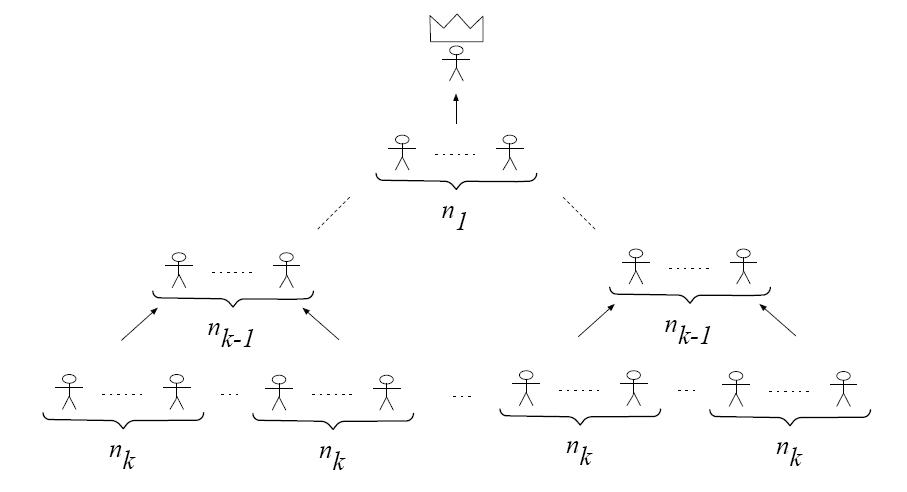
All electors are split into n₁ groups, all of equal size. Then each group is split into n₂ smaller sub-groups of equal size, where again n₂ is the same for all groups. Then each subgroup is split into n₃ equal sub-sub-groups, and so on, until level k, where the split is no longer possible. Each group at level i chooses by strict majority rule one candidate to represent the group at the higher level i – 1, and so on. Under the pressure of another relevant party, the “7 Planets Movement” that strongly supports the use of the web in democracy, the entire voting process, starting from the partition of the electors into subgroups, will be conducted electronically.

“Eureka!” – Tomboloni thinks – “I am not lost! If I will manage to control the electronic partitioning of electors, I will be able to organize the groups and distribute my supporters so that I will win the elections again!!! I just need to make an arrangement with the persons in charge of the partitioning process and I am done.”

Question. Do you think Tomboloni is right?

Wait a minute b4 reading the solution!!!

Yes, Tomboloni can really win the elections with so little support. Suppose in general that the number of electors is E. Write E as a product of non-trivial factors E = E_k = n₁ × n₂ × …× n_k. Then, if we let m_i = ⌊n_i∕2⌋ + 1 it is easy to see that S_k = m₁ × m₂ ×…× m_k supporters are sufficient in order to win the elections.

This can be proved by induction on k. The base case k = 1 is trivial. In fact, in this case E = n₁ and S = m₁ = ⌊n₁∕2⌋ + 1 is simply the strict majority of all the electors. For k > 0, we have to divide the electorate into E_k–1 = n₁ ×n₂ ×…×n_k–1 groups of size n_k. Since we are able to control the partitioning process, we can insert in S_k–1 = m₁ × m₂ ×…× m_k–1 of these groups m_k supporters of Tomboloni. After the vote, at level k – 1 there will be E_k–1 electors of which M_k–1 are supporters of Tomboloni. Hence we conclude by inductive hypothesis.

In the specific case, the total number of electors is 48,828,125 = 5¹¹. Hence, in order to win, Tomboloni just need 3¹¹ = 177,147 ≤ 200,000 supporters, much less than 1 percent!

One can observe that the technique above is not very robust: it will not work with a prime number of electors. That’s true, but it is not difficult to make it effective also in this case, by relaxing the requirement that all subgroups of electors should have the same size.

This is an adaptation of a puzzle which can be found at the “The Puzzle Toad” page of the Computer Science Department at Carnegie Mellon University (http://www.cs.cmu.edu/puzzle).

Disclaimer. All characters appearing in this puzzle are fictitious. Any resemblance to real persons, living or dead, is purely coincidental.