Marcello Balduccini, Eastman Kodak Company, USA
Michael Gelfond, Texas Tech University, USA

PDF Version.

Abstract
In this paper we give a summary of the Autonomous Agent Architecture (AAA architecture for short) for intelligent agents. The AAA architecture is the result of several years of research on the design and implementation of intelligent agents that reason about, and act in, changing environments. In the AAA architecture, the knowledge about the domain where the agent is situated is encoded in Answer Set Prolog and is shared by all of the reasoning components. The agent’s reasoning components are also formalized in Answer Set Prolog. Typical AAA agents are capable of observing the environment, interpreting the observations, recovering from unexpected observations, and planning to achieve their goals.

Introduction

The Autonomous Agent Architecture (AAA architecture for short) is an architecture for
the design and implementation of software components of intelligent agents reasoning
about, and acting in, a changing environment. The AAA architecture is based around
a control loop, called Observe-Think-Act Loop, consisting of the following steps:

1. Observe the world, explain the observations, and update the agent’s knowledge base;
2. Select an appropriate goal, G;
3. Find a plan (sequence of actions a1, . . . ,an) to achieve G;
4. Execute part of the plan, update the knowledge base, and go back to step 1.

Generally speaking, we view an architecture as a specification of (1) the agent’s control,
(2) the type and representation of the agent’s knowledge, and (3) how the basic
operations, or primitives (e.g. goal selection, planning), are performed. The agent’s
control for the AAA architecture is the Observe-Think-Act Loop. The representation
of knowledge and the execution of the primitives are based on the following assumptions:
(a) The world (including an agent and its environment) can be modeled by a
transition diagram whose nodes represent physically possible states of the world and
whose arcs are labeled by actions – the diagram therefore contains all possible trajectories
of the system; (b) The agent is capable of making correct observations, performing
actions, and remembering the domain history; (c) Normally the agent is capable of
observing all relevant exogenous events occurring in its environment. Notice that the
observations made at step 1 of the loop need not be complete, or taken at every iteration.
However, according to the assumptions just given, those observations must be
correct. The interested reader can refer to [21] for a study of reasoning algorithms that
can deal with wrong or false observations.
The knowledge of a AAA agent is encoded by a knowledge base written using
Answer Set Prolog (ASP) [17, 18, 11] and the Answer Set Programming methodology
[24]. At the beginning of this research, our original goal was in fact to investigate if the
knowledge representation capabilities of ASP could be used to represent the agent’s
knowledge, and if the primitives, such as diagnostics or planning, could be reduced
to reasoning with ASP. With time, we came to the realization that, although ASP is
sufficient in many situations, in some cases it is not. For these cases, we used CRProlog
[8, 2, 5] (whose development in fact is rooted in the research on the AAA
architecture) and P-log [13, 20, 14]. In the remainder of the discussion, whenever there
is no need to make a distinction, we loosely use the term “ASP” to refer to both the
original language and its extensions.
The AAA architecture was first suggested in [12]. Various reasoning algorithms
have been developed and refined along the years, most notably diagnostic reasoning
[7], planning [10], and inductive learning [3]. Throughout this paper we illustrate
the architecture and its use for agent design using the scenarios based upon a simple
electrical circuit. The domain is deliberately simple but we hope it is sufficient to
illustrate the basic ideas of the approach. Furthermore, in spite of the simplicity of the
domain used here, it is important to note that the corresponding algorithms are rather
scalable. In fact, they were successfully used in rather large, industrial size applications
[10].

Building the Action Description

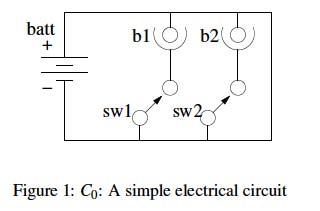
The electrical circuit that we will be referring to is depicted in Figure 1. Circuit C0
consists of a battery (batt), two safety switches (sw1, sw2), and two light bulbs (b1, b2).
By safety switches we mean switches with a locking device. To move a switch from its
current position, the switch must first be unlocked. The switch is automatically locked
again after it is moved. If all of the components are working properly, closing a switch
causes the corresponding bulb to light up.

Next, we describe in more detail how we model the circuit, and introduce some
useful terminology.
The state of the circuit is modeled by the following fluents (properties whose truth
changes over time): closed(SW): switch SW is closed; locked(SW): switch SW is
locked; on(B): bulb B is on; ab(B): bulb B is malfunctioning; down(BATT): battery
BATT has run down. When a fluent f is false, we write ¬f .
The agent interacts with the circuit by means of the following actions: f lip(SW):
move switch SW from open to closed, or vice-versa; unlock(SW): unlock SW;
replace(BATT), replace(B): replace a battery or a bulb.
We allow in the formalization actions whose occurrence is beyond the agent’s control
(e.g., a bulb blowing up). These actions are called exogenous. Relevant exogenous
actions for this domain are: run_down(BATT): battery BATT runs down; blow_up(B):
B blows up. Note that actions can occur concurrently. We distinguish between elementary
actions, such as the ones listed above, and compound actions, i.e. sets of
elementary actions, intuitively corresponding to the simultaneous execution of their
components. In the remainder of this paper we abuse notation slightly and denote
singletons by their unique component. We also use the term “action” to denote both
elementary and compound actions.
The behavior of the domain is described by laws. Depending upon the approach
used, the laws can be written using action languages [19] and later translated to ASP,
or encoded directly as ASP rules. To save space, here we adopt the direct encoding in
ASP. A possible encoding of the effects of actions unlock(SW) and close(B) is:

where variables SW, B, S range, respectively, over switches, bulbs, and non-negative
integers denoting steps in the evolution of the domain. The first law intuitively states
that unlocking SW causes it to become unlocked. This is called a direct effect of action
unlock(SW). Laws describing the direct effects of actions are usually called dynamic
laws. The second and third laws encode the effects of flipping a switch, and they, too, are dynamic laws.

The last law says that, if SW is closed and connected to some bulb
B in working order while the battery is not down, then B is lit. This law describes an
indirect effect, or ramification, of an action. Such laws are usually called static laws or
state constraints.
Similar laws encode the effects of the other actions and the behavior of malfunctioning
bulbs and battery. The encoding of the model is completed by the following
general-purpose axioms:

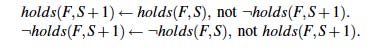where F ranges over fluents, S over steps. The rules encode the principle of inertia
“things normally stay as they are.”
Now, we turn our attention to the reasoning algorithms, and to the corresponding
agent’s behavior. For each reasoning algorithm, we select a scenario in which the main
reasoning algorithm used is the one of interest. (Because various steps of the Observe-
Think-Act loop are interconnected, most scenarios involve multiple algorithms.)

Planning Scenario

The idea of planning using Answer Set Programming dates back to [27, 15], where it
had been demonstrated that planning could be reduced to computing the answer sets
of suitable programs. What was not clear to us was if, and how, the approach could be
extended to medium and large sized applications. The conclusions of our research on
this issue, initially presented in [25] and later extended in [10], showed that the basic
planning technique had to be complemented with control knowledge [23, 22] in order
to improve the efficiency of planning in medium and large domains. We also showed
that such control knowledge could be easily encoded using ASP, as well as integrated
into the planner in an incremental fashion.

To understand how the ASP planning technique is tied into the AAA architecture,
consider the following scenario, based upon the domain introduced in the previous
section.

Example 1 Initially, all bulbs of circuit C0 are off, all switches open and locked, and
all components are working correctly. The agent’s goal is to turn on b1.

The intended agent behavior is as follows. At step 1 of the Observe-Think-Act loop,
the agent gathers observations about the environment. Recall that, in general, the observations
need not be complete, or taken at every iteration. Let us assume, however,
for simplicity that at the first iteration of the agent’s observations are complete. At step
2, the agent selects goal G=on(b1). At step 3, it looks for a plan to achieve G and finds
(unlock(sw1), flip(sw1)). Next, the agent executes unlock(sw1), records the execution
of the action, and goes back to observing the world.
Suppose the agent observes that sw1 is unlocked. Then, no explanations for the
observations are needed. The agent proceeds through steps 2 and 3, and selects the
plan ( f lip(sw1) ). Next, it executes f lip(sw1) and observes the world again. Let us
assume that the agent indeed discovers that b1 is lit. Then, the agent’s goal is achieved.

The key feature that allows exhibiting the described behavior is in the capability to
find a sequence of actions (a1, . . . ,ak) that achieves G. The task involves both selecting
the appropriate actions, and ordering them suitably. For example, the sequence of actions
(unlock(sw2), flip(sw1)) is not a good selection, while ( flip(sw1),unlock(sw1) )
is improperly ordered.
To determine if a sequence of actions achieves the goal, the agent uses its knowledge
of the domain to predict the effects of the execution of the sequence. This is
accomplished by reducing planning to computing answer sets of an ASP program,
consisting of the ASP encoding of the domain model, together with a set of rules informally
stating that the agent can perform any action at any time (see e.g. [26]).
This technique relies upon the fact that the answer sets of the ASP encoding of
the domain model together with facts encoding the initial situation and occurrence of
actions are in one-to-one correspondence with the corresponding paths in the transition
diagram. This result, as well as most of the results used in this and the next section, is
from [7]. We invite the interested reader to refer to that paper for more details. Simple
iterative modifications of the basic approach allow one to find shortest plans, i.e. plans
that span the smallest number of steps.
To see how this works in practice, let us denote by AD the action
description from the previous section, and consider a simple encoding,
O1, of the initial state from Example 1, which includes the facts
{holds(locked(sw1),0), ¬holds(closed(sw1),0), ¬holds(on(b1),0)} (more sophisticated
encodings are also possible). A simple yet general planning module PM1, which
finds plans of up to n steps, consists of the rule:

where A ranges over agent actions, S over steps, and cS denotes the current step (0 in
this scenario). Informally, the rule says that any agent action A may occur at any of the
next n steps starting from the current one. The answer sets of program P1 = AD∪O1∪
PM1 encode all possible trajectories, of length n, from the initial state. For example,
the trajectory corresponding to the execution of unlock(sw1) is encoded by the answer
set O1∪{occurs(unlock(sw2),0), ¬holds(locked(sw2),1), ¬holds(on(b1),1), . . . }.
Note that ¬holds(on(b1),1) is obtained from O1 and the inertia axioms.
To eliminate the trajectories that do not correspond to plans, we add to P1 the
following rules:

which informally say that goal on(b1) must be achieved. Let us denote the new
program by P1′.
It is not difficult to see that the previous set of literals is not
an answer set of P1′.
On the other hand, (if n ≥ 2) P1′
has an answer set containing
O1 ∪ {occurs(unlock(sw1),0),¬holds(locked(sw1),1),occurs( flip(sw1),1),
holds(closed(sw1),2),holds(on(b1),2)}, which encode the trajectory corresponding
to the execution of the sequence (unlock(sw1), flip(sw1)).

Interpretation Scenario

Another important feature of the AAA architecture is the agent’s ability to interpret
unexpected observations. Consider for instance the scenario:
Example 2 Initially, all of the bulbs of circuit C0 are off, all switches open and locked,
and all of the components are working correctly. The agent wants to turn on b1. After
planning, the agent executes the sequence (unlock(sw1), flip(sw1)), and notices that
b1 is not lit.
The observation is unexpected, as it contradicts the expected effects of the actions the
agent just performed. Intuitively, a possible explanation of this discrepancy is that b1
blew up while the agent was executing the actions (recall that all of the components
were initially known to be working correctly). Another explanation is that the battery
ran down. (Of course, it is always possible that the bulb blew up and the battery ran down, but we do not believe
this should be the first explanation considered by a rational agent.)
To find out which explanation corresponds to the actual state of the world, the agent
will need to gather additional observations. For example, to test the hypothesis that the
bulb blew up, the agent might check the bulb. Suppose it is found to be malfunctioning.
Then, the agent can conclude that blow_up(b1) occurred in the past. The fact that b1 is
not lit is finally explained, and the agent proceeds to step 3, where it re-plans.
The component responsible for the interpretation of the observations, often called
diagnostic component, is described in detail in [7]. Two key capabilities are needed
to achieve the behavior described above: the ability to detect unexpected observations,
and the ability to find sequences of actions that, had they occurred undetected in the
past, may have caused the unexpected observations. These sequences of actions correspond
to our notion of explanations.
The detection of unexpected observations is performed by checking the consistency
of the ASP program, Pd, consisting of the encoding of the domain model, together
with the history of the domain, and the Reality Check Axioms and Occurrence-Awareness Axiom, both shown below. The history is encoded by statements of the form
obs(F,S, truth_val) (where truth_val is either t or f , intuitively meaning “true” and
“false”) and hpd(A,S), where F is a fluent and A an action. An expression obs(F,S, t)
(respectively, obs(F,S, f )) states that F was observed to hold (respectively, to be false)
at step S. An expression hpd(A,S) states that A was observed to occur at S. The Reality
Check Axioms state that it is impossible for an observation to contradict the agent’s
expectations:

Finally, the Occurrence-Awareness Axiom ensures that the observations about the occurrences
of actions are reflected in the agent’s beliefs: occurs(A,S) ← hpd(A,S). It
can be shown that program Pd is inconsistent if-and-only-if the history contains unexpected
observations.
To find the explanations of the unexpected observations, the agent needs to search
for sequences of exogenous actions that would cause the observations (possibly indirectly),
if they had occurred in the past.

In the early stages of our research, we investigated reducing this task to reasoning
with ASP [6, 7]. Although the results were positive, we were not able to find an
elegant way to specify, in ASP, that diagnoses should be minimal. That led us to the
development of CR-Prolog [8, 2, 5], which solves the issue with minimal diagnoses
and, overall, allows for rather elegant, declarative formalizations.

In CR-Prolog, programs consist of regular ASP rules and of cr-rules. A cr-rule is
a statement of the form

where r is a (possibly
compound) term denoting the name of the cr-rule and li’s are ASP literals. The rule
intuitively says “if l1, . . . , lm hold and there is no reason to believe lm+1, . . . , ln, l0 may
possibly hold, but that happens rarely.” Informally, this possibility should be used only
if the regular rules alone are not sufficient to form a consistent set of beliefs. In the
CR-Prolog terminology, we say that cr-rules are used to restore consistency. The name
of the cr-rule is used in specifying preferences between cr-rules. The interested reader
can find more about preferences in [8].
As described in [10], the exogenous nature of an action e can be formalized in CRProlog
by one or more cr-rules of the form (cr-rules are not needed to encode the direct
and indirect effects of the action):

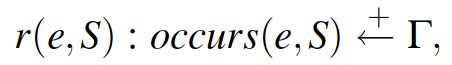where Gamma is a condition
under which the exogenous action may occur. The rule informally states that, under
those conditions, the exogenous action may possibly occur, but that is a rare event.
Then, let EX be the set of cr-rules:

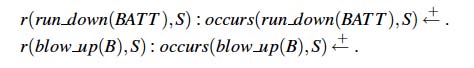informally stating that run down(BATT) and blow up(B) may possibly (but rarely)
occur. Consider now program P2 consisting of AD and the encoding of the initial state
O1 from the previous section, together with the Occurrence-Awareness Axiom, EX,
and the history H1 = {hpd(unlock(sw1),0), hpd( flip(sw1),1), obs(on(b1),2, f )}.
It is not difficult to show that the answer sets of P2 correspond to the set-theoretically
minimal explanations of the observations in H1. If no unexpected observation is present
in H1, the answer sets encode an empty explanation. Furthermore, specifying preferences
between cr-rules allows one to provide information about the relative likelihood
of the occurrence of the exogenous actions. More details can be found in [9].
In the next section, we discuss the specification of policies in the AAA architecture.

Policies and Reactivity

Here by policy we mean the description of those paths in the transition diagram that
are not only possible but also acceptable or preferable. The ability to specify policies
is important to improve both the quality of reasoning (and acting) and the agent’s
capability to react to the environment.
In this section we show how the AAA architecture, and in particular the underlying
ASP language, allows one to easily specify policies addressing both aspects.
We begin by considering policies allowing one to improve the quality of reasoning.
More details can be found in [1, 10]. In the circuit domain, one policy addressing
this issue could be “do not replace a good bulb.” The policy is motivated
by the consideration that, although technically possible, the action of replacing a
good bulb should in practice be avoided. A possible ASP encoding of this policy is
←occurs(replace(B),S),¬holds(ab(B),S). Note that, although the rule has the same
form as the executability conditions, it is conceptually very different. Also note that
this is an example of a strict policy because it will cause the action of replacing a good
bulb to be always avoided.
Often it is useful to be able to specify defeasible policies, i.e. policies that are
normally complied with but may be violated if really necessary. Such policies can be
elegantly encoded using CR-Prolog. For example, a policy stating “if at all possible,
do not have both switches in the closed position at the same time” can be formalized
as:

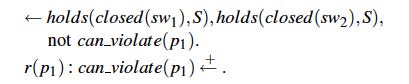The first rule says that the two switches should not be both in the closed position unless
the agent can violate the policy. The second rule says that it is possible to violate the
policy, but only if strictly necessary (e.g., when no plan exists that complies with the
policy).
Now we turn our attention to policies improving the agent’s capability to react to
the environment. When an agent is interacting with a changing domain, it is often
important for the agent to be able to perform some actions in response to a state of the
world. An example is leaving the room if a danger is spotted. Intuitively, selecting the
actions to be performed should come as an immediate reaction rather than as the result
of sophisticated reasoning. We distinguish two types of reaction: immediate reaction
and short reaction. Immediate reaction is when actions are selected based solely upon
observations. An example from the circuit domain is the statement “if you observe
a spark from closed switch SW, open it,” which can be formalized as (assume SW is
unlocked and fluent spark_from(SW) is available):

A short reaction is the occurrence of an action triggered by the agent’s beliefs.
This includes conclusions inferred from observations and possibly other beliefs.
An example is the statement “if a battery is failing, replace it,” encoded as:
occurs(replace(BATT),S) ← holds( f ailing(BATT),S). It is worth noting that similar
policies can also be used, in reasoning about multi-agent environments, to model
the behavior of the other agents [4].

Implementation of the AAA Architecture

A prototype that implements the AAA architecture is available from:
http://krlab.cs.ttu.edu/∼marcy/APLAgentMgr/. The program, called
APLAgent Manager, is implemented in Java and allows the user to specify observations (Figure 2), execute a number of iterations of the Observe-Think-Act
Loop, and inspect the agent’s decisions (Figure 3) and expectations about the future
(Figure 4). APLAgent Manager comes with pre-compiled implementations of the
Observe-Think-Act Loop, but also allows using a customized version of the loop.

When using the pre-compiled implementations of the Observe-Think-Act Loop,
APLAgent Manager expects the user to provide formalizations of the domain and of
the reasoning modules written in ASP (Figure 5). More information, as well as a
tutorial, can be found on the APLAgent Manager web page.

Conclusions

In this paper we have described an ASP-based architecture for intelligent agents capable
of reasoning about and acting in changing environments. The design is based upon
a description of the domain that is shared by all of the reasoning modules. The generation
and execution of plans are interleaved with detecting, interpreting, and recovering
from, unexpected observations. Although here we focused on explaining unexpected
observations by hypothesizing the undetected occurrence of exogenous actions, the architecture
has also been extended with a reasoning module capable of modifying the
domain description by means of inductive learning [3]. An initial exploration of the
issues of inter-agent communication and cooperation can be found in [16]. Dealing
with multiple, even prioritized, goals is also possible [4].

References

[1] Marcello Balduccini. USA-Smart: Improving the Quality of Plans in Answer Set
Planning. In PADL’04, Lecture Notes in Artificial Intelligence (LNCS), Jun 2004.
[2] Marcello Balduccini. CR-MODELS: An Inference Engine for CR-Prolog. In
LPNMR 2007, pages 18–30, May 2007.
[3] Marcello Balduccini. Learning Action Descriptions with A-Prolog: Action Language
C. In Eyal Amir, Vladimir Lifschitz, and Rob Miller, editors, Procs of
Logical Formalizations of Commonsense Reasoning, 2007 AAAI Spring Symposium,
Mar 2007.
[4] Marcello Balduccini. Solving the Wise Mountain Man Riddle with Answer Set
Programming. In Ninth International Symposium on Logical Formalizations of
Commonsense Reasoning (Commonsense09), 2009.
[5] Marcello Balduccini. Splitting a CR-Prolog Program. In 10th International Conference
on Logic Programming and Nonmonotonic Reasoning, Sep 2009.
[6] Marcello Balduccini, Joel Galloway, and Michael Gelfond. Diagnosing physical
systems in A-Prolog. In Proceedings of the 6th International Conference on Logic
Programming and Nonmonotonic Reasoning, pages 213–225, Sep 2001.
[7] Marcello Balduccini and Michael Gelfond. Diagnostic reasoning with A-Prolog.
Journal of Theory and Practice of Logic Programming (TPLP), 3(4–5):425–461,
Jul 2003.
[8] Marcello Balduccini and Michael Gelfond. Logic Programs with Consistency-
Restoring Rules. In Patrick Doherty, John McCarthy, and Mary-Anne Williams,
editors, International Symposium on Logical Formalization of Commonsense
Reasoning, AAAI 2003 Spring Symposium Series, pages 9–18, Mar 2003.
[9] Marcello Balduccini and Michael Gelfond. The AAA Architecture: An
Overview. In AAAI Spring Symposium 2008 on Architectures for Intelligent
Theory-Based Agents (AITA08), Mar 2008.
[10] Marcello Balduccini, Michael Gelfond, andMonica Nogueira. Answer Set Based
Design of Knowledge Systems. Annals ofMathematics and Artificial Intelligence,
2006.
[11] Chitta Baral. Knowledge Representation, Reasoning, and Declarative Problem
Solving. Cambridge University Press, Jan 2003.
[12] Chitta Baral and Michael Gelfond. Reasoning Agents In Dynamic Domains. In
Workshop on Logic-Based Artificial Intelligence, pages 257–279. Kluwer Academic
Publishers, Jun 2000.
[13] Chitta Baral, Michael Gelfond, and Nelson Rushton. Probabilistic Reasoning
with Answer Sets. In Proceedings of LPNMR-7, pages 21–33, Jan 2004.
[14] Chitta Baral, Michael Gelfond, and Nelson Rushton. Probabilistic reasoning with
answer sets. Journal of Theory and Practice of Logic Programming (TPLP),
2005.
[15] Yannis Dimopoulos, J. Koehler, and B. Nebel. Encoding planning problems in
nonmonotonic logic programs. In Proceedings of the 4th European Conference on
Planning, volume 1348 of Lecture Notes in Artificial Intelligence (LNCS), pages
169–181, 1997.
[16] Gregory Gelfond and Richard Watson. Modeling Cooperative Multi-Agent Systems.
In Proceedings of ASP’07, pages 67–81, Sep 2007.
[17] Michael Gelfond and Vladimir Lifschitz. The stable model semantics for logic
programming. In Proceedings of ICLP-88, pages 1070–1080, 1988.
[18] Michael Gelfond and Vladimir Lifschitz. Classical negation in logic programs
and disjunctive databases. New Generation Computing, pages 365–385, 1991.
[19] Michael Gelfond and Vladimir Lifschitz. Action Languages. Electronic Transactions
on AI, 3(16), 1998.
[20] Michael Gelfond, Nelson Rushton, and Weijun Zhu. Combining Logical and
Probabilistic Reasoning. In AAAI 2006 Spring Symposium, pages 50–55, 2006.
[21] Nicholas Gianoutsos. Detecting Suspicious Input in Intelligent Systems using
Answer Set Programming. Master’s thesis, Texas Tech University, May 2005.
[22] Y. Huang, H. Kautz, and B. Selman. Control Knowledge in Planning: Benefits
and Tradeoffs. In Proceedings of the 16th National Conference of Artificial
Intelligence (AAAI’99), pages 511–517, 1999.
[23] H. Kautz and B. Selman. The Role of Domain-Specific Knowledge in the Planning
as Satisfiability Framework. In Proceedings of AIPS’98, 1998.
[24] Victor W. Marek and Miroslaw Truszczynski. The Logic Programming
Paradigm: a 25-Year Perspective, chapter Stable models and an alternative logic
programming paradigm, pages 375–398. Springer Verlag, Berlin, 1999.
[25] Monica Nogueira, Marcello Balduccini, Michael Gelfond, Richard Watson, and
Matthew Barry. An A-Prolog decision support system for the Space Shuttle. In
Alessandro Provetti and Tran Cao Son, editors, Answer Set Programming: Towards
Efficient and Scalable Knowledge Representation and Reasoning, AAAI
2001 Spring Symposium Series, Mar 2001.
[26] Monica Nogueira, Marcello Balduccini, Michael Gelfond, Richard Watson, and
Matthew Barry. An A-Prolog decision support system for the Space Shuttle. In
PADL 2001, pages 169–183, 2001.
[27] V. S. Subrahmanian and Carlo Zaniolo. Relating Stable Models and AI Planning
Domains. In Proceedings of ICLP-95, 1995.